高等数学基本定理（证明）及推论

在高等数学中，有时求极限，用带Peano余项的Taylor公式代换的方法求，许多高等数学教材中都有例子，但都没有说明取到哪一项才合适，因此，这一点必须弄清楚，如若不然，生搬、仿照去用此法，可能就会出现错误，故此，下面给出定理.

定理1.3.1 设α1±α2及β是x→x0时的无穷小，α2＝f（x0）＋f′（x0）（x－的充要条件是n≥k.

证 （充分性）因（c是常数），故β与（x－x0）k是同阶无穷小（x→x0），当n≥k时，因o（（x－x0）n）＝o（β）又α2＝Pn（x）＋o（（xx0）n），故

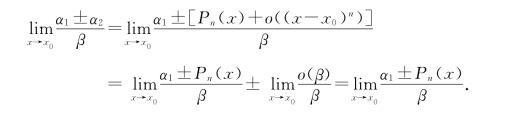
（必要性）若，则

故α2－Pn（x）＝o（β），即o（（x－x0）n）＝o（β），又β与（x－x0）k是同阶无穷小（x→x0），所以n≥k.

推论1.3.1　设α1及β1±β2是x→x0时的无穷小，β2＝Pn（x）＋o（（xx0）n），如果（c是常数，k是正整数）存在且不等于零，则的充要条件是n≥k.

证 由定理1.3.1知的充要条件是n≥k，也就是的充要条件，即的充要条件.

定理1.3.2 设α1，α2，β均为x→x0时的无穷小，α2＝Pn（x）＋o（（xx0）n存在，如果（c是常数，k是正整数），则的充分条件是n≥k－1.

证 因，故β与（x－x0）k是同阶无穷小，当n≥k－1时，o（（x－x0）n）＝O（β）（x→x0），即有界.又α2＝Pn（x）＋o（（x－x0）n），所以

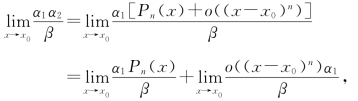
又α1是无穷小，所以

推论1.3.2 α，β1，β2均为x→x0时的无穷小，β2＝Pn（x）＋o（（x－x0）n），如果（c是常数，k是正整数）存在且不等于零，则的充分条件是n≥k－1.

证 由定理1.3.2知的充分条件是n≥k－1，也就是的充分条件，即的充分条件.

注 k为非整正数时，定理1.3.1的结论为n≥［k＋1］；定理1.3.2的结论为n≥［k］.