【摘要】：幂级数是高等数学中的重要内容之一，在这部分内容中经常要求幂级数的收敛半径或收敛域，一般都用达朗贝尔判别法，亦可用柯西判别法求得，其两个定理如下：定理 设幂级数，则幂级数的收敛半径定理 如果对幂级数，则此幂级数的收敛半径由于两个定理都可求幂级数的收敛半径，所以，我们可以从中得到有用的结论，因此，下面给出定理.定理1.4.1 如果φ＞0且存在，则.证 令，因此，以an（n＝0，1，2，…
幂级数是高等数学（或数学分析）中的重要内容之一，在这部分内容中经常要求幂级数的收敛半径或收敛域，一般都用达朗贝尔（D’Alembert）判别法，亦可用柯西（Cauchy）判别法求得，其两个定理如下：
定理（Cauchy判别法） 设幂级数
，则幂级数
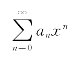的收敛半径
定理（D’Alembert判别法） 如果对幂级数
，则此幂级数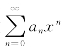
的收敛半径
由于两个定理都可求幂级数的收敛半径，所以，我们可以从中得到有用的结论，因此，下面给出定理.
定理1.4.1 如果φ（n）＞0且
存在，则
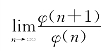（n为自然数）.
证 令
，因此，以an（n＝0，1，2，…）为系数可得到幂级数
又
存在，即
存在，故由D’Alembert判别法知：幂级数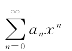
的收敛半径为
存在，则由参考文献［1］中的引理9.3.1知
一定存在，即
存在.所以由Cauchy判别法得：幂级数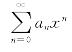
的收敛半径
如果
，则R是一确定的常数，所以，
，故
如果
，则R＝＋∞，所以
故此，
因此，
定理1.4.2 设φ（x）当x大于某一正数时有定义，φ（x）＞0且
均存在，则
证 设n＝［x］，则
存在，故可设
A，则∀ε＞0，∃X＞0，当x＞X时，恒有
.因x＞X，故n＞［X］时，亦有
成立，所以
因此，
又同理可证
由定理1知
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
