高等数学中多元函数的定理（证明）及推论

多元函数的极限在高等数学中是非常重要的内容之一，但由于多元函数的自变量多，因此，对于判断其极限存在与否及其求法，比起一元函数的极限就显得比较困难，故此，我们可运用球面坐标把多元函数极限转化为一元函数极限来求，就此作一初步探讨.

定理1.5.1 设f（x，y，z）在点（0，0，0）的某去心邻域内有定义，则

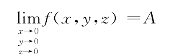
的充要条件是：恒有取值无关的一确定常数.

证 （必要性）若

则对于任意给定的ε＞0，一定存在δ＞0，当时，就有｜f（x，y，z）－A｜＜ε恒成立.直角坐标与球面坐标关系是

当不论θ，φ取何值，都有0＜r＜δ，所以｜f（rcosθsinφ，rsinθsinφ，rcosφ）－A｜＝｜f（x，y，z）－A｜＜ε，故rcosφ）＝A.

（充分性）如果不论θ，φ取何值，恒有A，则对于任意给定的ε＞0，一定存在δ＞0，当0＜r＜δ时，恒有成立.只要0＜r＜δ，就有0＜，故｜f（x，y，z）－A｜＝｜f（rcosθsinφ，rsinθsinφ，rcosφ）－A｜＜ε恒成立，所以

当时，则有z≡0.就得到：

＊当r沿曲线趋向0时，θ，φ也是变化的.

推论1.5.1 设f（x，y）在点（0，0）的某去心邻域内有定义，则的充要条件是：恒有为与θ取值无关的一确定常数.

定理1.5.2 设f（x，y，z）在点（x0，y0，z0）的某去心邻域内有定义，则

的充要条件是：恒有为与θ，φ取值无关的一确定常数.

证 作变换

故当x→x0，y→y0，z→z0时，x′→0，y′→0，z′→0.所以

由定理1.5.1知的充要条件是：恒有为与θ，φ取值无关的一确定常数.即为的充要条件.当z≡0时，就得到：

推论1.5.2 设f（x，y）在点（x0，y0）的某去心邻域内有定义，则的充要条件是：恒有为与θ取值无关的一确定常数.