【摘要】：对于第二型曲面积分，如果有向曲面Σ的方程为z＝z（x，y）或y＝y（z，x），x＝x（y，z），计算上面的曲面积分都比较复杂，因此，下面给出直接用二重积分计算的方法.定理2.9.1 设有向曲面Σ（取上侧）是由方程z＝z（x，y）给出的，Σ－表示曲面取下侧，且Σ在xOy坐标面上的投影区域为Dxy，z＝z（x，y）在Dxy上具有一阶连续偏导数，P（x，y，z），Q（x，y，z），R（x，y，z）在Σ上
对于第二型曲面积分
，如果有向曲面Σ的方程为z＝z（x，y）或y＝y（z，x），x＝x（y，z），计算上面的曲面积分都比较复杂，因此，下面给出直接用二重积分计算的方法.
定理2.9.1 设有向曲面Σ（取上侧）是由方程z＝z（x，y）给出的，Σ－表示曲面取下侧，且Σ在xOy坐标面上的投影区域为Dxy，z＝z（x，y）在Dxy上具有一阶连续偏导数，P（x，y，z），Q（x，y，z），R（x，y，z）在Σ上连续，则
证 （1）由于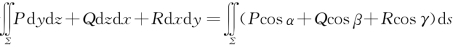
，又Σ表示取上侧的曲面，则可取
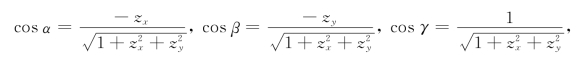
所以有
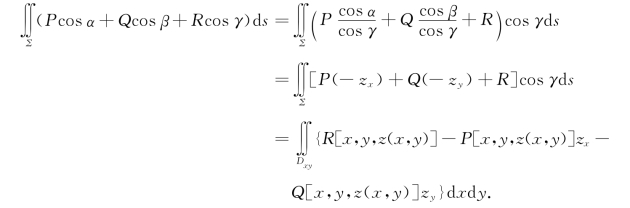
即
（2）当积分曲面为Σ－时，
则有
如果Σ（表示取右侧或前侧）的方程为y＝y（z，x）或x＝x（y，z）时，可得到相应的计算公式
或
如果积分曲面为Σ－时与上面积分仅差一个符号.
定理2.9.2 设Γ为分段光滑的空间有向闭曲线，Σ（取上侧）是以Γ为边界的分片光滑有向曲面，其方程为z＝z（x，y），且Γ的正方向与Σ的法向量符合右手法则，P，Q，R在Σ（连同边界Γ）上具有一阶连续偏导数，z＝z（x，y）在Σ的投影区域Dxy上也具有一阶连续偏导数，则
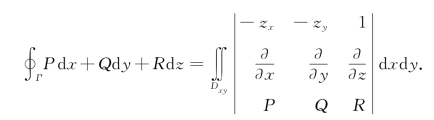（即Stokes公式的二重积分形式）
证 由Stokes公式可得
由于Σ的方程为z＝z（x，y），故由定理2.9.1的（1）得
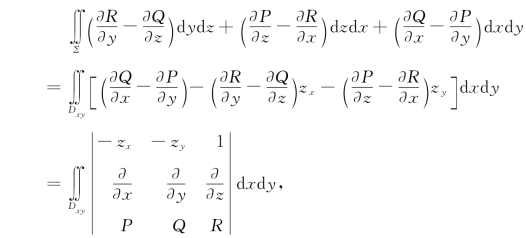
即
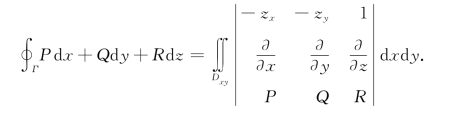
如果Σ（表示取右侧或前侧）的方程为y＝y（z，x）或x＝x（y，z）时，得到相应的计算公式
或
如果以Γ为边界的分片光滑有向曲面为Σ－时与上面积分也仅差一个符号.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
