工程项目的不确定性经济分析

各个方案技术经济变量（如投资、成本、产量、价格等）受政治、文化、社会因素、经济环境、资源与市场条件、技术发展情况等因素的影响，而这些因素是随着时间、地点、条件的改变而不断变化的，这些不确定性因素在未来的变化就构成了项目决策过程的不确定性。同时项目经济评价所采用的数据一般都带有不确定性，加上主观预测能力的局限性，对这些技术经济变量的估算与预测不可避免地会有误差，从而使投资方案经济效果的预期值与实际值可能会出现偏差。这种情况通称为工程项目的风险与不确定性。

产生不确定性与风险的原因主要有主观和客观两个方面。

1）不确定性与风险产生的主观原因

（1）信息的不完全性与不充分性。

（2）人的有限理性等。

2）不确定性与风险产生的客观原因

（1）市场供求变化的影响。

（2）技术变化的影响。

（3）经济环境变化的影响。

（4）社会、政策、法律、文化等方面的影响。

（5）自然条件和资源方面的影响等。

美国经济学家奈特认为风险是“可测定的不确定性”，而“不可测定的不确定性”才是真正意义上的不确定性。工程项目风险分析就是分析工程项目在其环境中的寿命期内自然存在的导致经济损失的变化，而工程项目不确定性分析就是对项目风险大小的分析，即分析工程项目在其存在的时空内自然存在的导致经济损失之变化的可能性及其变化程度。

从理论上讲，风险是指由于随机原因引起的项目总体的实际价值对预期价值之间的差异。风险是与出现不利结果的概率相关联的，出现不利结果的概率（可能性）越大，风险也就越大。而不确定性是指以下两方面。

（1）对项目有关的因素或未来的情况缺乏足够的情报而无法做出正确的估计。

（2）没有全面考虑所有因素而造成的预期价值与实际价值之间的差异。

所以，从理论上可以区分风险与不确定性，但从项目经济评价角度来看，试图将它们绝对分开没有多大意义，实际上也无必要。

风险与不确定性管理成为工程项目管理的一个重要内容，风险与不确定性分析是项目风险管理的前提与基础。通过分析方案各个技术经济变量（不确定性因素）的变化对投资方案经济效益的影响（还应进一步研究外部条件变化如何影响这些变量），分析投资方案对各种不确定性因素变化的承受能力，进一步确认项目在财务和经济上的可靠性，这个过程称为风险与不确定性分析。这一步骤作为工程项目财务分析与国民经济分析的必要补充，有助于加强项目风险管理与控制，避免在变化面前束手无策。同时，在风险与不确定性分析基础上做出的决策，可在一定程度上避免决策失误导致的巨大损失，有助于决策的科学化。

工程经济分析人员应善于根据各项目的特点及客观情况变化的特点，抓住关键因素，正确判断，提高分析水平。工程经济分析中不确定性分析的基本方法包括盈亏平衡分析、敏感性分析和概率分析。盈亏平衡分析只用于财务效益分析，敏感性分析和概率分析可同时用于财务效益分析和国民经济效益分析。

盈亏平衡是指当年的销售收入扣除销售税金及附加后等于其总成本费用，在这种情况下，项目的经营结果既无盈利又无亏损。盈亏平衡分析是通过计算盈亏平衡点BEP（break-even point）处的产量或生产能力利用率，分析拟建项目成本与收益的平衡关系，来判断拟建项目适应市场变化的能力和风险大小的一种分析方法。所以，盈亏平衡分析也称量本利分析。盈亏平衡点是项目盈利与亏损的分界点，它标志着项目不盈不亏的生产经营临界水平，反映在一定的生产经营水平时工程项目的收益与成本的平衡关系。

对于盈亏平衡分析模型而言，按成本、销售收入和产量之间是否呈线性关系可分为线性盈亏平衡分析和非线性盈亏平衡分析。

1. 线性盈亏平衡分析

线性盈亏平衡分析一般基于以下三个假设条件来进行。

（1）产品的产量与销售量是一致的。

（2）单位产品的价格保持不变。

（3）成本分为可变成本与固定成本，其中可变成本与产量成正比，固定成本与产量无关，保持不变。

此时，产品的产量（Q）、固定成本（CF）、可变成本（CV）、销售收入（S）、利润（E）之间的关系如图4-7所示。

图4-7　产品产量、固定成本、可变成本、销售收入、利润间的关系

由图4-7可得出以下公式。

总成本　　C=CF+CV×Q　　（4-90）

销售收入　　S＝（单价P－单位产品税金t）×Q　　（4-91）

当P-t一定时，S随Q的增加成比例增加，即呈线性变化。当P-t不定时，S不单只取决于Q，还要考虑P-t这时呈非线性变化。

利润为　　E=S-C=（P-t）Q-（CF+CV×Q）=（P-t-CV）Q-CF　　（4-92）

此时，对应产量　　Q=（E+CF）/（P-t-CV）　　（4-93）

在盈亏平衡点BEP处，Q=Q*（盈亏平衡产量），项目处于不盈不亏的状态，也即是项目的收益与成本相等，即S=C，E=S-C=0，有

Q=Q*=CF/（P-t-CV）　　（4-94）

盈亏平衡点（BEP）除经常用产量表示外，可以用生产能力利用率f，单位产品价格等指标P表示如下。

f*=Q*/Q0×100%　　（4-95）

式中，Q0为设计生产能力。

P*（单位产品价格）=f*/ Q0+V+t　　（4-96）

所以，Q*值越小越好，同样f*越小越好，说明工程项目抗风险能力越强，亏损的可能性越小。

【例4-9】　某企业拟新建一个工厂，拟定了A、B、C三种不同方案。经过对各方案进行的分析预测，三种方案的成本结构数据见表4-9。若预料市场未来需求量在15 000件左右，试选择最优方案。

表4-9　方案A、B、C的成本结构数据表

【解】　CA=300 000+40Q，CB=500 000+20Q，CC=700 000+30Q。

令CA=CB，即300 000+40Q=500 000+20Q，解得QA=10 000件

令CB=CC，即500 000+20Q=700 000+10Q，解得QB=20 000件

而预测产量为15 000件，则应选AB线段之间，即CB的线段。

故应选方案B为最优方案，如图4-8所示。

图4-8　盈亏平衡分析图

2. 非线性盈亏平衡分析

在实际生产经营过程中，产品的销售收入与销售量之间，成本费用与产量之间，并不一定呈现出线性关系，在这种情况下进行盈亏平衡分析称为非线性盈亏平衡分析。例如，当产量达到一定数额时，市场趋于饱和，产品可能会滞销或降价，这时呈非线性变化；而当产量增加到超出已有的正常生产能力时，可能会增加设备，要加班时还需要加班费和照明费，此时可变费用呈上弯趋势，产生两个平衡点BEP1和BEP2，如图4-9所示。

图4-9　非线性盈亏分析图

非线性盈亏分析的基本过程如下。

（1）产量Q<Q1*或Q>Q2*时，项目都处于亏损状态。

（2）产量Q1*<Q<Q2时，项目处于盈利状态。

因此，Q1、Q2是项目的两个盈亏平衡点的产量。

又已知利润表达式如下。

利润=收益-成本=S-C

通过求上式对产量的一阶导数并令其等于零，即可得

d[（S-C）]/dQ=0

从而可以求出利润为最大的产量Qmax。

【例4-10】　已知固定成本为60 000元，单位变动成本为35元，产品单价为60元。由于成批采购材料，单位产品变动成本可减少1‰；由于成批销售产品，单价可降低3.5‰；求利润最大时的产量。

【解】　总成本　　C（q）=60 000+（35-0.001q）q

总收入　　F（q）=（60-0.003 5q）q

令C（q）=F（q），则　　0.002 5q2-25q+60 000=0

解得　　q1=4 000，　q2=6 000

又因为　　E（q）=F（q）-C（q）=-0.002 5q2+30q-60 000

令d[E（q）]/dq=0，则q=6 000。

因d2[E（q）]/dq2=-0.005<0，所以6 000是利润最大时的产量。

盈亏平衡分析的主要目的在于通过盈亏平衡计算找出和确定一个盈亏平衡点，以及进一步突破此点后增加销售数量、增加利润、提高盈利的可能性。盈亏平衡分析还能够有助于发现和确定企业增加盈利的潜在能力以及各个有关因素变动对利润的影响程度。通过盈亏平衡分析，可以看到产量、成本、销售收入三者的关系，预测经济形势变化带来的影响，分析工程项目抗风险的能力；从而为投资方案的优劣分析与决策提供重要的科学依据。但是由于盈亏平衡分析仅仅是讨论价格、产量、成本等不确定因素的变化对工程项目盈利水平的影响，却不能从分析中判断项目本身盈利能力的大小。另外，盈亏平衡分析是一种静态分析，没有考虑货币的时间价值因素和项目计算期的现金流量的变化，因此，其计算结果和结论是比较粗略的，还需要采用其他的能分析判断出因不确定因素变化而引起项目本身盈利水平变化幅度的、动态的方法进行不确定性分析。

在许多情况下，只对方案进行盈亏平衡分析是不够的，它只能通过变动售价、产量、成本等因素所导致的盈亏平衡点或线发生变化来进行不确定性分析。

1. 敏感性分析的作用与基本原理

所谓敏感性分析，从广义上来说，就是研究单一影响因素的不确定性给经济效果所带来的不确定。具体说来，就是研究某一拟建项目的各个影响因素（售价、产量、成本、投资等）在所指定的范围内变化，而引起其经济效果指标（如投资的内部收益率、利润、回收期等）的变化。敏感性就是指经济效果指标对其影响因素的敏感程度的大小。对经济效果指标的敏感性影响大的那些因素，在实际工程中要严加控制和掌握，而对于敏感性较小的那些影响因素，在实际工程中只需稍加控制即可。

因此，敏感性分析是研究分析项目的投资、成本、价格、产量和工期等主要变量发生变化时，导致对项目经济效益的主要指标发生变动的敏感程度。工程经济分析中的财务分析指标主要是项目内部收益率、净现值、投资收益率、投资回收期或偿还期，敏感性分析也称为灵敏度分析。

通过敏感性分析，可以在诸多的不确定因素中，找出对经济效益指标反应敏感的因素，并确定其影响程度。计算出这些因素在一定范围内变化时，有关效益指标变动的数量，从而建立主要变量因素与经济效益指标之间的对应定量关系（变化率），进而可绘制敏感性分析图（见图4-10）。同时，可求出各因素变化的允许幅度（极限值），计算出临界点，考察其是否在可接受的范围之内。敏感性分析是侧重于对最敏感的关键因素（即不利因素）及其敏感程度进行分析。

图4-10　敏感性分析示意图

敏感性分析通常是分析单个因素的变化，必要时也可分析两个或多个不确定因素的变化对项目经济效益指标的影响程度。因此，除了采用单因素变化的敏感性分析以外，还可采用多因素变化的分析等。项目对某种因素的敏感程度，可表示为该因素按一定比例变化时引起项目指标的变动幅度（列表表示）；也可表示为评价指标达到临界点（如财务内部收益率等于财务基准收益率，或是经济内部收益率等于社会折现率）时，某个因素允许变化的最大幅度，即极限值。敏感性分析可以使决策者了解不确定因素对项目经济效益指标的影响，从而提高决策的准确性，还可以启发工程经济分析人员对那些较为敏感的因素重新进行分析研究，以提高预测的可靠性。通过进行项目的敏感性分析，可以研究各种不确定因素变动对方案经济效果的影响范围和程度，了解工程项目方案的风险根源和风险大小，还可筛选出若干最为敏感的因素，有利于对它们集中力量研究，重点调查和收集资料，尽量降低因素的不确定性，进而减少方案风险。另外，通过敏感性分析，可以确定不确定因素在什么范围内变化时能使项目的经济效益情况最好；并确定在什么范围内变化时，项目的经济效益、情况最差等这类最乐观和最悲观的边界条件或边界数值。

2. 敏感性分析的一般步骤

进行敏感性分析的一般步骤如下。

（1）确定敏感性分析指标。如净现值、内部收益率等。

（2）选取不确定因素。

（3）固定其他因素，变动其中某一个不确定因素，逐个计算不确定因素对分析指标的影响程度（或范围），并找出它们的一一对应关系。

（4）找出敏感因素。

（5）对方案进行综合方面分析，实施控制弥补措施。

下面通过实例来说明这种方法。

【例4-11】　某企业拟建一个预制构件厂，其产品是大板结构住宅的预制板，该厂需投资20万元，每天可生产标准预制板100 m2，单价为140元/m3，每年生产350天，生产能力利用程度可达到80%，寿命期为20年，基准收益率为12%，对其进行敏感性分析。

【解】　年度收入：　100×350×140×0.8万元=392万元

年度支出：

①折旧费=20×（A/P，12%，20）万元=2.677 6万元

②人工费=54万元

③经常费=（4+4）万元=8万元

④材料费=0.8×100×350×115万元=322万元

在经常费中，固定费用和可变费用各占一半，为简单起见，试分析各因素的变化对静态投资收益率的影响。以下以生产能力利用程度、产品售价、使用寿命三个因素为例进行敏感性分析。

①当其生产能力利用程度为80%时，各项指标计算如下。

● 年度总收入=392万元

● 年度总支出＝386.677 8万元

● 利润=5.322 4万元

● 投资收益率=5.322 24/20=26.6%

②当生产能力利用程度为70%时，各项指标计算如下。

● 年度总收入=100×350×140×0.7万元=343万元

● 年度总支出＝345.927 6万元

● 利润=-2.927 6万元

● 投资收益率=-2.9276/20=-14.64%

● 其中材料费=100×350×11×0.7万元=281.75万元

● 经常费=（4+3.5）万元=7.5万元

说明：由于在生产能力利用程度为80%时，经常费中的可变费用为4万元，由此可计算出当生产能力利用程度为100%时，其经常费中的可变费用为4/0.8万元=5万元。因此，当生产能力利用程度为70%时，其经常费就为（4+70%×5）万元，而其中的固定费，不论生产能力利用程度为多少，始终不变。

表4-10为几种生产能力利用程度的具体计算结果。由此可知，生产能力利用程度对收益率的影响很敏感，工厂投产后要严加控制。可尝试改变某些因素，重新确定其各项费用，使之变成不敏感因素。

表4-10　生产能力敏感分析

敏感性分析侧重于对不利因素及其影响程度的分析。除以上单个因素分析外，必要时，可分析两个或多个不确定因素对投资风险的影响程度。单因素的敏感分析适用于分析最敏感的因素，但它忽略了各因素之间的相互作用，因为多因素的估计误差所造成的风险一般比单个因素较大。因此在对项目进行风险分析时，除了要进行单因素的敏感性分析外，还应进行多因素的敏感性分析，下面仅就双因素情况进行敏感性分析。一次改变一个因素的敏感性分析可以得到敏感性曲线，若分析两个因素同时变化的敏感性，则可以得到一个敏感面。

【例4-12】　某企业为了研究一项投资方案，提出了下面的因素指标估计（见表4-11），见下表。假定最关键的敏感因素是投资和年销售收入，试同时进行这两个参数的敏感性分析。

表4-11　某企业的投资指标估计

【解】　以净年金A*为研究目标，设X为初始投资变化的百分数，设Y为初始年收入变化的百分数，则净年金A*为

A*=-10 000（1+X）（A/P，i，n）+5 000（1+Y）（A/P，i，n）-2 200+2 000（A/F，i，n）

将i=8%，n=5代入可得

A*=636.32+5 000Y-2 504.6X

临界曲线为A*=0，则Y=0.500 92X-0.127 264，作图如下。

作图后，就得到如图4-11所示的两个区域，其中所希望的区域（A*>0）占优势。如果预计造成±20%的估计误差，则净年金对增加投资额比较敏感。例如，若投资增加5%，年销售收入减小12%，则A*<0。

图4-11　两个参数的敏感性分析

3. 敏感性分析的局限性

敏感性分析是项目经济评价时经常用到的一种方法，是投资决策中的两个重要步骤之一。它在一定程度上对不确定因素的变动对项目投资效果的影响做了定量的描述，得到了维持投资方案在经济上可行所允许的不确定因素发生不利变动的最大幅度，但是敏感性分析在使用中也存在着一定的局限性，就是它不能说明不确定因素发生变动的情况的可能性是大还是小，也就是没有考虑不确定因素在未来发生变动的概率，而这种概率是与项目的风险大小密切相关的。

1. 基本原理

由于盈亏平衡分析和敏感性分析只是假定在各个不确定因素发生变动可能性相同的情况下进行的分析，而忽略了它们是否发生和发生可能的程度有多大等问题。因此只有概率分析才能明确这类问题。

概率是指事件的发生所产生某种后果的可能性的大小。概率分析是在选定不确定因素的基础上，通过估计其发生变动的范围，然后根据已有资料或经验等情况，估计出变化值下的概率，并根据这些概率的大小，来分析测算事件变动对项目经济效益带来的结果和所获结果的稳定性，它是一种定量分析方法。同时，又因为事件的发生具有随机性，故概率分析又称为简单风险分析。

2. 概率分析方法

概率法是在假定投资项目净现值的概率分布为正态的基础上，通过正态分布图像面积计算净现值下小于零的概率，来判断项目风险程度的决策分析方法。这种分析方法适用的前提条件是项目每年现金流量独立，即上年的现金收回情况好坏并不影响本年的现金收回，本年的现金收回也不影响下年的现金收回。

概率法首先要计算期望净现值E（NPV），具体公式如下。

其次，要计算项目的现金流量标准差σ，具体公式如下。

最后，计算NPV小于零的概率并判断项目风险大小和项目的可行性，其一般计算步骤如下。

（1）列出各种应考虑的不确定因素，如投资、经营成本、销售价格等。

（2）设想各种不确定因素可能发生的变化情况，即确定其数值发生变化个数。

（3）分别确定各种情况出现的可能性及概率，并保证每个不确定因素可能发生的情况的概率之和为1。

（4）分别求出各种不确定因素发生变化时，方案净现值流量各状态发生的概率和相应状态下的净现值的期望值。

（5）求出净现值大于或等于零的累计概率。

（6）对概率分析结果作出说明。

【例4-13】　某企业评价的某项目之可能的各年净现金流量和该公司约定的CV-d换算表见表4-12，若Ic=8%，试求E（NPV）并判断其可行性。

表4-12　净现金流量和CV-d换算表

【解】　先求出各个σ值，为此计算各年的E（Nt）。

E（N0）=-10 000×1.0=-10 000

E（N1）=4 500×0.3+5 000×0.4+6 500×0.3=5 300

E（N2）=4 000×0.3+6 000×0.2+7 000×0.4=5 200

E（N3）=3 000×0.25+5 000×0.5+8 000×0.2=4 850

再求各年净现金流量的σ。

σ0=0

σ1=[（4 500-5 000）2×0.3+（5 000-5 000）2×0.4+（6 500-5 000）2×0.3]1/2=866.0

σ2=[（4 000-6 000）2×0.3+（6 000-6 000）2×0.2+（7 000-6 000）2×0.4]1/2=1 264.9

σ3=[（3 000-5 000）2×0.25+（5 000-5 000）2×0.50+（8 000-5 000）2×0.2]1/2=1 673.3

至此，可以计算出期望净现值相当于项目现金流量标准差的倍数为

Z=E（NPV）/σ=3 215.7/1 893=1.70

根据Z值，可从正态分布表中，查得正态分布图像边上尖交面积对应的百分数，这就是项目的净现值小于零的概率P，如图4-12所示。

图4-12　年净现值概率分布

经查表得Pb=0.034 1，这一结果如图4-12所示，即NPV<0的概率仅为3.41%，风险是很小的。

由公式Z=E（NPV）/σ可知，E（NPV）越大，σ越小，Z值就越大；Z值越大，Pb就越小，项目就越有吸引力，反之则结论相反。

3. 期望值决策方法

1）净现值期望值的数学含义

式中　NPVi——第i种状态的净现值；

n——自然状态数；

Pi——第i种状态的概率。

2）期望值进行决策必须具备以下条件

（1）目标。

（2）几个可行方案。

（3）所对应的自然状态。

（4）概率。

（5）相应的可计算出的损益值——加权平均值。

【例4-14】　某土方工程，施工管理人员要决定下个月是否开工，若开工后遇天气不下雨，则可按期完工，获利润6万元，遇天气下雨，则要造成1.5万元的损失。假如不开工，不论下雨还是不下雨都要付窝工费1 000元。据气象预测下月天气不下雨的概率为0.3，下雨概率为0.7，利用期望值的大小为施工管理人员做出决策。

【解】　开工方案的期望值　E1=60 000×0.3元+（-15 000）×0.7元=7 500元

不开工方案的期望值　E2=（-1 000）×0.3元+（-1000）×0.7元=-1 000元

因为E1>E2，则应选开工方案。

1. 基本形式

可以将例4-9决策内容绘制成如图4-13所示的决策树。其中，图中“□”代表决策点，从决策点画出的每一条直线代表一个方案，称为方案枝；“〇”代表机会点（也可称为概率分枝点），从机会点画出的每一条直线代表一种自然状态，称为概率分枝；“△”为可能结果点，代表各种自然状态下的可能结果。

图4-13　决策树方法基本形式

【例4-15】　某公司拟建设一个预制构件厂，一个方案是大厂，需要359万元，另一个方案是小厂，需要160万元，使用期均为10年。另外，方案在不同自然状态下的损益值及自然状态概率见表4-13，试利用决策树法决策。

表4-13　损益值及自然状态概率

决策树图形如图4-14所示，各点期望值如下。

点1　　0.7×100×10万元+0.3×（-20）×10万元-359万元=281万元

点2　　0.7×40×10万元+0.3×10×10万元-160万元=150万元

两者相比较，可知建大厂较优，10年期望值为281万元。

图4-14　例4-11决策树

2. 多级决策问题

【例4-16】　由例4-11，现已现建小厂，如销路好，则第三年后扩建，扩建投资需要140万元，扩建后可使用7年，每年损益值与大厂相同。此方案与建大厂方案相比较，何者较优？画出的决策树图如图4-15所示，大厂方案未变化，仍将其损益期望值写在节点1之下。

图4-15　例4-12决策树

【解】　计算各节点的损益期望值。

点6　　0.9×100×7+0.1×（-20）×7-140=476

点7　　0.9×40×7+0.1×10×7=259

比较点6及点7，扩建方案优于不扩建方案，决策节点Ⅱ的损益期望值即为扩建方案的期望值476万元。

点5　　1.0×10×7=70

点2　　0.7×40×3+0.3×10×3+0.7×476+0.3×70-160=287.2

既建小厂方案的损益期望值为287.2，高于建大厂方案。最优策略即为先建小厂，如销路好3年后再扩建。如将建厂投资的利息计入，则这个方案的优越性更大。

从例4-12可以看出，利用决策树法计算多级决策，既方便又直观。

1. 贝叶斯概率方法的基本特点

自从20世纪50～60年代贝叶斯（Bayes）学派形成后，关于贝叶斯分析的研究久盛不衰。20世纪80年代后，贝叶斯网络就成功地应用于专家系统，成为表示不确定性专家知识和推理的一种重要的方法。

贝叶斯决策属于风险型决策，决策者虽不能控制客观因素的变化，但却可以掌握其变化的可能状况及各状况的分布概率，并利用期望值即未来可能出现的平均状况作为决策准则。由于决策者对客观因素变化状况的描述不确定，所以在决策时会给决策者带来风险。但是完全确定的情况在现实中几乎不存在，贝叶斯决策不是使决策问题完全无风险，而是通过其他途径增加信息量使决策中的风险减小。由此可以看出，贝叶斯决策是一种比较实际可行的方法。

利用贝叶斯所提出的概率理论，我们可以考察决策的敏感性。贝叶斯提出了先验概率和后验概率的概念，故可以根据新的信息对先验概率加以修改从而得出后验概率。因此，贝叶斯理论被用于将新信息结合到分析当中。

根据贝叶斯方法，已知：

（1）状态先验概率P（wi）（i=1，2，…，c）。

（2）类条件概率密度P（x|wi）（i=1，2，…，c）。

利用贝叶斯公式：

可得到状态的后验概率P（wi|x）。

2. 应用举例

将贝叶斯概率理论与决策树方法结合起来使用，则及时根据市场信息可以建立一个解决风险型投资决策的模型方法。

【例4-17】　某房地产公司打算聘请一个咨询公司来调查市场情况。这项调查的花费为5 000元。该公司是否应选择这一方式？这样做将导致改变公司对市场情况预测的先验概率。该公司查阅了咨询公司的历史业绩记录，其结果见表4-12。该表显示当市场实际增长时，该咨询公司的70%的报告预见到了这一增长，同时20%的报告预见的是市场将保持稳定，而10%的报告则预测的是市场将衰退。表4-14中的其他数据的含义与此类似。

表4-14　初始预测表

【解】　贝叶斯定理就是利用这些信息来修正有关的先验概率。假设有r个互斥事件Wi（i=1，2，…，r），其先验概率为P（Wi）。进一步假设有事件Fk，在事件Wi发生的前提下事件Fk发生的概率为P（Fk/Wi）。那么如果我们知道Fk已发生，则事件Wi发生的概率即为：

如果有i个互斥事件Wi（i=1，2，…，r），仅当其中一个事件发生后，事件F才能发生，则在事件F已知时，事件Wj发生的概率为

式中　P（Wi）——事件Wi的先验概率；

P（Fk/Wj）——假定Wj发生，事件Fk发生的条件概率；

P（Wj/Fk）——假定Fk发生，事件Wj的后验概率。

在例4-13中，各结果的先验概率为

W1—增长→P（W1）=0.6

W2—稳定→P（W2）=0.3

W3—衰退→P（W3）=0.1

如果Fr是指一个调查，该调查表明市场实际增长，从表4-5中我们可以知道当预测报告预计市场将增长时，其结果为0.7的可能增长，0.2的可能不变，0.1的可能衰退。

因此可得

P（Fr/W1）=0.7

P（Fr/W2）=0.2

P（Fr/W3）=0.1

利用贝叶斯（Bayes）公式，在预测报告预计市场增长条件下，市场实际出现增长的概率为

市场报告改变了各结果的概率，贝叶斯（Bayes）概率见表4-15。

表4-15　修正后的预测表

这样就可画出一个新的决策树。对其的求解是从期望收益来推算最初的目标。底层的方案枝是原来的决策树。但是只有在获得预计市场增长、不变或衰退的报告的概率已知后，才可对其求解。

获得一个预计市场增长的报告的概率就是在各种市场情况下得出市场增长预测报告的概率乘以各种市场情况出现的概率。因此获得一个预测市场增长的报告的概率为

P=（0.7）（0.6）+（0.2）（0.3）+（0.1）（0.1）=0.49

类似地，获得一个预测市场不变的报告的概率为0.32，而获得一个预测市场衰退的报告的概率为0.19。现在将这些值代入到决策树中，咨询公司报告的预期收益是：

EP=（0.49）（219.6）+（0.32）（168.0）+（0.19）（141.1）=18 817

因为获得该报告须花费5 000元，故净收益为13 817元，这少于没有报告时的收益，因此该公司无法从咨询报告中获得益处。这一点如图4-16中利用贝叶斯（Bayes）分析所制定的决策树所示。

图4-16　根据贝叶斯（Bayes）理论绘制的决策树

3. 贝叶斯决策规则的选择

应用贝叶斯分析方法，决策者可根据具体情况和决策意愿选择不同的决策规则。

1）基于最小错误率的贝叶斯决策规则

在决策问题中，人们往往希望尽量减小错误，从这样的要求出发，利用贝叶斯公式，就能得出使错误为最小的分类规则，称之为基于最小错误率的贝叶斯决策。

2）基于最小风险的贝叶斯决策规则

在基于最小错误率的贝叶斯分类决策中，使错误率P（e）达到最小是重要的。但实际上有时须要考虑一个比错误率更为重要的广泛的概念——风险。风险和损失是紧密联系的，最小风险贝叶斯决策正是考虑各种错误造成损失不同而提出的一种决策规则，在此决策中利用了决策论的观点进行考虑。在已知先验概率P（wi）及类条件概率密度P（x|wi）（i=1，2，…，c）的条件下，在考虑错判所造成的损失时，由于引入“损失”的概念，而必须考虑所采取的决策是否使损失最小。

3）最小最大的贝叶斯决策规则

从最小错误率和最小风险贝叶斯决策中可以看出其决策都是与先验概率P（w1）有关的。如果给定的x，其P（w1）不变，按照贝叶斯决策规则，可以使错误率和风险最小。但是如果P（w1）是可变的，或事先对先验概率毫不知道的情况下，若再按某个固定的P（w1）条件下的决策进行就往往得不到最小错误率或最小风险。而最小最大决策就是考虑在P（w1）变化的情况下，如何使最大可能的风险为最小，也就是在最差的条件下争取到最好的结果。

贝叶斯决策属于风险型决策，决策者虽不能控制客观因素的变化，但却可掌握其变化的可能状况及各状况的分布概率。将贝叶斯概率分析与决策树方法相结合，并利用期望值作为决策准则的依据，这为贝叶斯方法在投资风险决策的应用提出了一种可行方法。在此基础上可根据需要选择相关决策规则实现风险决策目标。

模拟是风险分析的一种深层次的方法，其本质是一种统计试验方法。蒙特卡罗分析（Mont carlo method）是随机模拟的一种形式，称其为蒙特卡罗法是因为该方法利用随机数来对各种可能结果进行选择，正如在轮盘赌中是通过小球所停的位置来确定赢家，其理论上也是一种随机现象。在建筑业中，可以模拟不同的天气类型以确定它们对施工进度的影响。同样，模拟技术也可以用于对工程项目费用的评价工作。

蒙特卡罗模拟要求生成多组随机数来对各种方案进行考察。可以用多种方法来确定随机数，如从帽子中抓阄或掷骰子。在实际工作中，利用计算机程序来生成多组随机数是最有效的方法。

模拟的前提是可以用概率分布来对受不确定性影响的参数加以描述。在蒙特卡罗模拟中，生成了大量的项目假想情况来反映实际项目的特征。每一个模拟（或重复）是通过用从一个风险变量的概率分布中抽取的一个随机数来代表该变量而实现的。通常须进行至少100次重复以建立整体项目的频率分布，然后利用统计的方法来计算其置信区间等，部分结果通常也用累计频率曲线来表示。通过这些曲线，可以较容易地得出一个特定工作按时完成的可能性，如图4-17所示。

图4-17　累计频率曲线

【例4-18】　某建设公司投标竞争一项建设项目，据预测该建设项目可能建设期为5年、8年、10年的概率分别为0.2，0.5，0.3，为承建此建设项目需购置一部专用设备，有两个厂家提供了如表4-16的资料，试用仿真模拟试验来选购设备（假设年折算利率为8%）。

表4-16　设备费用资料

【解】　先对工程工期、设备年费用列出其概率与二位随机数范围表，见表4-17。

表4-17　工程工期、设备年费用概率和二位随机数范围表

进一步对工程工期进行仿真试验，假设进行10次试验。即先任意指定第一个随机数，然后连续取9个随机数（从二值随机数表上按行或列均可）。如70，14，18，48，82，58，48，78，51，28。然后计算两设备购买费的费用年金（即投资分摊），现将计算结果列在表4-18之中。

表4-18　甲、乙两设备购买费费用年金（即投资分摊）
单位：万元

在上述基础上，对设备甲进行仿真试验10次。从随机数表中任意抽取一组（10个）随机数，再从表4-19中查出对应的年设备费用，将结果列在表4-20之中。同时对设备乙也可进行类似的仿真试验，将结果也列在表4-20之中。

表4-19　设备仿真实验年设备费用表
单位：万元

将表4-18中两设备费用年金（即投资分摊）分别和表4-19中两设备各自仿真试验年费用相加。即可得到甲、乙两设备仿真试验总费用年金。将结果列在表4-20之中。

表4-20　费用计算表
单位：万元

甲设备费用年金10年平均值为124.29万元，乙设备费用年金10年平均值为115.73万元，按经济评价准则应选用费用年金小的乙设备。

在应用蒙特卡罗法进行经济分析时，要注意随机事件的概率描述应当是古典概率型。在仿真试验时，从随机数表上抽取随机数时应当是任意的，不可心存任何偏见，试验次数应该尽可能多，这样试验所得结果才较为可靠。

【例4-19】　某公司经营情况如下：房租为300元/月，假设经营产品A、B、C的利润各占总利润的1/3，现通过对A的销售来对方案进行可行性分析，假设A的平均进价为1.50元/斤，售价为1.70元/斤，平均每月销售A约3 000斤，每月进货2次，运费150元/次，水电费60元/月，免税收。试分析A公司的各项指标。

1. 盈亏平衡分析

固定成本：A的固定成本占总固定成本的1/3。

F=（300+2×150+60）元=220元

盈利：　TR=（P-t）Q=（1.7-0）Q=1.7Q

成本：　TC=F+VQ=220+1.5Q

由TC=TR，得

盈亏平衡销售量斤/月=1100斤/月

盈亏平衡曲线如图4-18所示。

图4-18　盈亏平衡分析图

最低销售率=1 100/3 000×100%=36.7%

2. 作敏感度分析

销售量的敏感度为（±10%，±20%）

月收入：　1.7×3 000元=5 000元

月支出：

月材料费：　1.5×3 000元=4 500元

故总额为380元，销售量的敏感度分析见表4-21。

表4-21　销售量的敏感度分析表

售价的敏感度见表4-22。

表4-22　售价的敏感度分析表

进价的敏感度如见表4-23。

表4-23　进价的敏感度分析表

运费的敏感度见表4-24。

表4-24　运费的敏感度分析表

以上四方面因素分析如图4-19所示。

图4-19　销售量、售价、进价、运费的敏感度分析图

根据以上分析，决策人就可以对方案作出比较全面合理的判断，由图4-19可以清楚地看出月收入对于进价和售价的变化都很敏感，而对于月销售量和运费则不敏感。

3. 概率分析

假设售价和销售量的概率关系如图4-20所示。

图4-20　假设售价和销售量的概率关系

计算其联合概率，见表4-25。

表4-25　联合概率

由表可以看出，除去月使用费和月材料费220元，每月A的销售利润为406.7元。根据计算结果，该方案虽然利润不多，但风险很小，决策者可以选择投资。

1. 什么是基本建设和基本建设程序？

2. 可行性研究作用是什么？其基本内容有哪些？

3. 市场调查的基本程序和方法是什么？

4. 试分析比较一般工业项目和道路工程项目可行性研究的特点。

5. 财务评价的主要目的是什么？

6. 固定资产的投资估算主要有哪几种方法？

7. 流动资金估算应注意什么问题？

8. 什么是工程项目的国民经济评价？它与财务评价有何异同？

9. 根据国民经济评价和财务评价的结论，工程项目的取舍标准是什么？

10. 国民经济评价中费用与效益的识别原则是什么？

11. 什么是直接效益、直接费用和间接效益、间接费用？

12. 需要单独考虑和计算的外部效果有哪些？

13. 什么是转移支付？常见的转移支付有哪些？

14. 试从国民经济评价角度列出下列工程项目的效益与费用：高速公路、卷烟厂及果园。

15. 在国民经济评价中采用的经济参数主要有哪些？

16. 什么是影子价格？在国民经济评价中为什么要用影子价格来度量工程项目的费用与效益？

17. 什么是影子汇率、影子工资、社会折现率、贸易费用率？它们的取值是如何确定的？

18. 什么是外贸货物和非外贸货物？它们的影子价格是如何确定的？

19. 什么是土地的影子价格？它的组成部分包括什么？

20. 国民经济评价的指标主要有哪些？它们的判别标准各是什么？

21. 如何理解风险和不确定性的特征和产生原因？

22. 不确定性分析的常用方法有哪些？各自适用条件是什么？

23. 利用盈亏平衡分析进行生产决策？影响盈亏平衡点的主要因素有哪些？

24. 敏感性分析法的一般程序是怎样的？如何选择敏感性分析指标？

25. 决策树决策的依据和基本条件是什么？

1. 某软件历年需求量的发生值如表4-26所示，试求2004年的需求量。

表4-26　某软件历年需求量
单位：套

2. 已知某化工厂的某种产品1999—2004年的销售额如表4-27所示，单位为万元，分别以自变量xi代表年，因变量yi代表销售额（单位为万元），试预测2005年的销售额。

表4-27　某化工厂产品历年销售额

3. 拟新建某工业项目，生产国内市场上需求量较大的化工产品F，生产规模为年产1万吨。主要技术和设备在国内购进，厂址位于城市近郊，占用农田100亩，交通便利，原材料、燃料及水电等供应可靠。该项目包括生产车间及相应的辅助生产设备、生产管理和生活福利等设施的建设。拟2年建成，第3年投产，当年生产负荷达到设计能力的60％，第4年达到80%，第5年达到100%。生产期按10年计算，计算期为12年。

（1）固定资产投资估算。

项目的固定资产投资估算数为1 200万元，其中工程费用1 010万元，其他费用90万元（其中土地费用70万元），预备费用100万元（包括基本预备费90万元和涨价预备费10万元）。

项目的固定资产投资方向调节税计税依据为固定资产投资额，税率为10％，因此投资方向调节税为120万元。

项目建设期利息估算为30万元。

（2）流动资金估算。

项目的流动资金是按分项详细估算法进行估算的。项目所需流动资金400万元，分别于投产期第3年和第4年各投200万元。

（3）投资计划与资金筹措。

项目自有资金850万元，其中用于第1年固定资产投资550万元，第2年固定资产投资200万元，第4年流动资金投入100万元。其余为借款共900万元，其中从建设银行借款600万元，利率为10%，用于第2年固定资产投资；从工商银行借款300万元，利率为8%，用于第3年、第4年流动资金投入，分别为200万元、100万元。

（4）固定资产折旧费估算。

项目的固定资产原值为1 330万元，固定资产形成率是按100%考虑的。化工厂项目按平均年限法计算折旧，折旧年限为10年，预计净残值为50万元。

（5）无形及递延资摊销费估算。

项目递延资产为20万元（固定资产投资中的其他费用扣除土地费用），摊销年限为10年，年摊销费为2万元。该项目没有无形资产投入。

（6）主要产出物和投入物价格的估算。

项目主要产出物和投入物的价格，是以近几年国内市场已实现的价格为基础，考虑到其变化趋势预测得到的。化工厂项目的主要产出物和投入物价格依据见表4-28。

表4-28　主要产出物和投入物使用价格依据表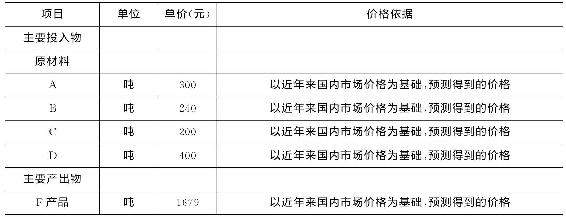

表4-29　单位产品生产成本估算表
单位：元

（7）单位产品生产成本估算。

估算单位产品生产成本，首先要列出单位产品生产成本的构成项目（如原材料、燃料和动力、工资与福利费、制造费用及副产品回收等），根据单位产品的消耗定额和单价估算单位产品生产成本，见表4-29。

（8）总成本费用估算。

化工厂项目的总成本费用估算表中各项估算说明如下。

①外购原材料、外购燃料及动力、折旧费、摊销费和利息支出，依据有关报表填列。

②除第3年外全厂定员100人（第3年定员66人），每年工资及福利费为95万元（第3年为63万元）。

③修理费按年折旧费的55%计取，每年约为70万元。

④其他费用按工资及福利费的两倍多再加土地使用税10万元计算。

（9）借款还本付息计算。

化工厂项目固定资产投资借款600万元，年利率10%，建设期利息以自有资金偿还，生产期利息计入财务费用，本金以与银行商定的等额本金法偿还，分别在第4年至第7年各偿还本金150万元。偿还本金的资金来源分别为各年未分配利润30万元、年折旧费118万元和年摊销费2万元。

（10）产品销售收入和销售税金及附加估算。

化工厂项目产品销售收入的估算值在生产负荷为60%、80%、100%时分别为1 007万元、1 343万元、1 679万元；销售税金及附加的估算值在生产负荷为60%、80%、100%时分别为114万元，153万元、191万元。试对该项目进行财务评价，并且编制有关财务报表。

4. 已知某出口产品的影子价格为1 480元/吨，国内的现行市场价格为1 000元/吨，试求该产品的价格换算系数。

5. 已知某项目产出物在距项目所在地最近的口岸的离岸价格为50美元/吨，影子汇率为8.76元人民币/美元，项目所在地距口岸300公里，国内运费为0.06元/吨·公里，贸易费用率按离岸价格的6%计算，试求该项目产出物出厂价的影子价格。

6. 某进口产品的国内现行市场价格为800元/吨，其价格换算系数为2.2，国内运费和贸易费用为120元/吨，影子汇率为8.76元人民币/美元，试求该进口产品的到岸价格。

7. 某企业年固定成本为300万元，产品单价150元/台，单位产品可变成本240元，求盈亏平衡产量。

8. 某项目年总成本C=2X-8X+16，产品单价P=5-Q/8，Q为产量，求盈亏平衡产量。

9. 某企业年固定成本6.5万元，每件产品变动成本25元，原材料批量购买可降低单位材料费用为购买量的0.1%，每件售价为55元，随销售量的增加市场单位产品价格下降0.25%，试计算盈亏平衡点、利润最大时产量和成本最低时的产量。

10. 某沿河岸台地铺设地下管道工程施工期内（1年）有可能遭到洪水的袭击，据气象预测，施工期内不出现洪水或出现洪水不超过警戒水位的可能性为60%，出现超过警戒水位的洪水的可能性为40%。施工部门采取的相应措施：不超过警戒水位时只需进行洪水期间边坡维护，工地可正常施工，工程费约10 000元。出现超警戒水位时为维护正常施工，普遍加高堤岸，工程费约70 000万元。工地面临两个选择：①仅做边坡维护，但若出现超警戒水位的洪水工地要损失10万元。②普遍加高堤岸，即使出现警戒水位也万无一失。试问应如何决策？

11. 某公司打算购进一种新设备，有两个代理商提出报价资料见表4-30，假设折算年利率为10%，试用仿真试验进行决策。

表4-30　某设备报价资料表