设备的经济寿命的影响因素有哪些

设备的经济寿命是指设备从投入使用开始到因继续使用在经济上不合理而被更新所经历的时间。

设备的经济寿命是由设备维护费用的提高和使用价值的降低决定的。设备使用年限越长，所分摊的设备年资产消耗成本越少。但是随着设备使用年限的增加，一方面需要更多的维修费维持原有功能；另一方面设备的操作成本及原材料、能源耗费也会增加，年运行时间、生产效率、质量将下降。因此，年资产消耗成本的降低，会被年度运行成本的增加或收益的下降所抵消。在整个变化过程中存在着某一年份，设备年平均使用成本最低，经济效益最好，如图5-4所示，在N0年时，设备年平均使用成本达到最低值。我们称设备从开始使用到其年平均使用成本最小（或年盈利最高）的使用年限N0为设备的经济寿命。所以，设备的经济寿命就是从经济观点（即成本观点或收益观点）确定的设备更新的最佳时刻。

图5-4　设备年度费用曲线图

设备寿命期限的影响因素主要有：设备的技术构成、设备成本、加工对象、生产类型、工作班次、操作水平、产品质量、维护质量和环境要求。设备经济寿命的确定方法有静态模式和动态模式两种。

静态模式下设备经济寿命的确定方法，就是在不考虑资金时间价值的基础上计算设备年平均使用成本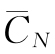，使得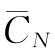最小的N0就是设备的经济寿命。静态模式下设备经济寿命的计算方法常用的有两种，即公式计算法和列表计算法。

1. 公式计算法

当不考虑资金的时间价值时，设备经济寿命的计算公式如下。

式中　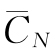——N年内设备的年平均使用成本；

P——设备目前实际价值，如果是新设备则包括购置费和安装费，如果是旧设备则包括旧设备现在的市场价值和继续使用旧设备追加的投资；

Ct ——第t年的设备运行成本，包括人工费、材料费、能源费、维修费、停工损失费、废次品损失等；

LN——第N年末的设备净残值。

在式（5-9）中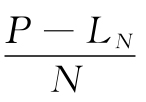，为设备的平均年度资产消耗成本，而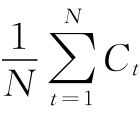为设备的平均年度运行成本。

在式（5-9）中，如果使用年限N为变量，则当N0（0<N0≤N）为经济寿命时，应满足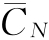最小。

【例5-1】　某设备目前实际价值为3万元，有关统计资料如表5-1所示，求其经济寿命。

表5-1　某设备运行有关资料
单位：元

【解】　由统计资料可知，该设备在不同使用年限时的年平均成本如表5-2所示。

表5-2　设备在不同使用年限时的静态模式下的年平均成本
单位：元

由表5-2可知，当设备使用到第5年时，年平均使用成本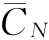=13 500元为最小，也即当设备一共使用5年，每年的年平均使用成本最低，因此可以认为设备在不考虑资金时间价值的情况下其经济寿命为5年。

2. 列表计算法

由式（5-1）和表5-2可知，用设备的年平均使用成本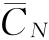估算设备的经济寿命的过程为：在已知设备现金流量的情况下，逐年计算出从寿命1年到N年全部使用期的年平均使用成本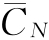，从中找出年平均使用成本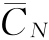的最小值及其所对应的年限，从而确定设备的经济寿命。

由于设备的使用时间越长，设备的有形磨损和无形磨损越来越加剧，从而导致设备的维护修理费用增加越多，这种逐年递增的费用ΔCt称为设备的低劣化。用低劣化数值表示设备损耗的方法称为低劣化数值法。如果每年设备的劣化增量是均等的，即ΔCt=λ，每年劣化呈线性增长。假设评价基准年（即评价第一年）设备的运行成本为C1，则平均每年的设备使用成本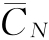可以用下式表示。

要使得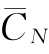为最小，设LN为一常数（如果LN不为常数且无规律可循时，需用列表法计算），对上式的N进行一阶求导，并令其导数为零，则可将上式简化为如下形式。

式中　N0 ——设备的经济寿命；

λ——设备的低劣化值。

【例5-2】　假定有一台设备，目前实际价值P=8 000元，预计残值LN=800元，第一年的设备运行成本Q=600元，每年设备的劣化增量是均等的，年劣化值λ=300元，求该设备的经济寿命。

【解】　（1）列表法计算设备经济寿命。

列表计算各年的年平均使用成本，如表5-3所示。

表5-3　用低劣化数值法计算设备经济寿命
单位：元

由表5-3可知，当设备使用年限为7年的时候，年平均使用成本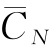=2 529元为最小，因此可以认为该设备的经济寿命即为7年。也就是说该设备使用7年，每年的平均成本是最低的，如果接着使用该设备，那么继续使用该设备的能源费、保养费、修理费、停工损失费、废次品损失费等各种费用总和将比更新该设备的年平均费用更高，因此这个时候最合理的就是更新该设备。

（2）公式法计算设备经济寿命。由式（5-10）可得：

也即该设备的经济寿命为7年，与列表法计算所得的结果相一致。

【例5-3】　某设备的原始价值为10 000元，自然寿命为10年，第一年的运行成本为700元，劣化值、年末残值等变化如表5-4所示，试计算该设备的经济寿命。

【解】　经济寿命计算如表5-4所示。

表5-4　某设备经济寿命计算表
单位：元

由表5-4可知，当设备使用年限为8年的时候，年平均使用成本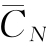=2 326元为最小，因此可以认为该设备的经济寿命即为8年。

由例5-3可知，当设备每年的劣化值不等时，我们无法用简化计算公式来计算设备的经济寿命，因此，这种情况下，一般采用列表法计算设备的经济寿命。虽然列表法计算设备经济寿命相对于公式法来说步骤较多，比较麻烦，但是其结果准确，思路清晰，是初学者经常采用的方法。

动态模式下设备经济寿命的确定方法，就是考虑资金时间价值的基础上计算设备最佳的更新时期。

1. 单利条件下设备经济寿命的计算

假定设备的年运行成本的劣化是线性增长的，第一年的运行成本为C1，每年运行成本增加额为λ，若设备使用了N年，则第N年时的运行成本CN为

CN=C1+（N-1）λ

显然，N年内设备的运行成本的平均值将为

除运行成本外，在设备的年均费用中还有每年分摊的年资金费用，其金额为: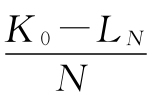

另外，还要考虑单利情况下，设备占有资金的利息为：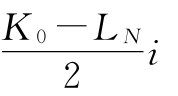

式中　i——银行利息。

设备的年总费用则为

求AC的最小值。利用导数的知识，上式对N求导，并令其等于零，可得

若不考虑设备的残值，其经济寿命和最小年均费用为

【例5-4】　假定某设备初始投资为200万元，残值为零，运行费用第一年为4万元，以后每年递增1万元，利率为10%，试计算该设备的经济寿命及最小年均费用。

【解】　由式（5-11）得，其经济寿命为

2. 复利条件下设备经济寿命的计算

考虑资金时间价值，并以复利计算，年总费用平均值不是算术平均值，而是指时间调整为平均，即先把各年的费用折算成现值，然后再将其看做是年金总额的现值，乘以资金收回系数，得到年金各年支付额，即为年均总费用的时间调整的平均值。

式中　λ——劣化值；

（A/P，i，n）——资金回收系数；

（A/F，i，n）——偿债基金系数；

（P/F，i，n）——一次支付现值系数。

在给定的基准折现率i时，令AC最小，此时对应的年限就是设备在考虑资金时间价值情况下的经济寿命。