成本曲线与成本曲线的关系:短期成本

如前所述，短期内某些生产要素是固定不变的，可变的仅仅是一部分生产要素。与此相对应，厂商对固定要素的投入，其支付为固定成本或不变成本；对可变要素的投入，其支付为可变成本。由此，厂商在短期内的总成本由固定成本和可变成本两部分组成。

总成本（total cost，TC）是指厂商在生产规模不变条件下生产一定量产出所需的最低成本的总额，它由固定成本和可变成本两部分组成。

固定成本（fixed cost，FC）是指厂商在短期内对固定不变的生产要素进行的支付，它不随产量的变动而变动，属于既定生产规模下的固定费用。

可变成本（variable cost，VC）是指厂商在短期内为可变的生产要素进行的支付，它随着产量的变动而变动，是产量的函数。

TC=FC+VC

TC=Φ（Q）+b

在上述的总成本函数中，b表示固定成本，与产量无关；Φ（Q）表示可变成本，是产量的函数。

与上述总成本相对应，在短期内存在着三种平均成本，即平均固定成本、平均可变成本和平均成本。

平均固定成本（average fixed cost，AFC）为每单位产品所摊付的总固定成本，其公式可表示为

AFC=FC/Q

平均变动成本（average variable cost，AVC ）为每单位产品所摊付的变动成本，其公式可表示为

AVC=VC/Q

平均成本（average cost，AC）为每单位产品所摊付的总成本，其公式可表示为

AC=TC/Q=AFC+AVC

边际成本（marginal cost，MC ）为增加一单位产品生产和销售所引起的总成本的变化量，其公式可表示为

MC=dTC/dQ

为了说明上述成本之间的关系，我们举一个假设的例子。假设有一成本函数为

TC=Q³-12Q²+60Q+40

则

VC=Q³-12Q²+60Q

AC=Q²-12Q+60+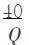，FC=40

MC=3Q²-24Q+60

当Q从0开始变化时，我们可以得到如表5-1所示的相关数据。

表5-1　各项短期成本数据

图5-1　成本曲线

依据表5-1的各项短期成本数据，我们可以绘制出成本曲线，如图5-1所示。从中我们可以看出：

VC曲线：从原点出发，先递减增长，到达拐点（B点）之后转而递增增长。

FC曲线：与产量无关，是平行于横轴的直线。

TC（VC＋FC ）曲线：VC上移FC的距离，先递减增长，再递增增长，拐点为A点，在B点垂直上方。

AVC与VC：原点与VC曲线上点的连线的斜率就是AVC。

AC与TC：原点与TC曲线上点的连线的斜率就是AC。

MC与TC（VC）：TC（VC）曲线上点的切线的斜率就是MC。

AFC与FC：固定不变的FC随产量的增加，其与产量的比值越来越小，即为AFC。

AVC、AC、MC都呈U形；AFC向右下方倾斜，无穷趋近横轴。

MC上升阶段先后与AVC、AC最低点相交；AC、AVC随产量的增加而趋向接近；AC、AVC间的垂直距离就是AFC。

边际成本与平均变动成本之间的关系：当边际成本小于平均变动成本时，平均变动成本随产量的增加而减少；当边际成本大于平均变动成本时，平均变动成本随产量的增加而增加；当边际成本等于平均变动成本时，平均变动成本为最小值。

我们可以通过数学公式的推导对上述结论加以证明。

附：成本函数与生产函数之间的关系

生产函数决定了成本函数曲线的形状；投入要素的价格决定了成本函数曲线的位置。以一种变动投入要素的生产系统为例：

由于成本函数与生产函数之间存在以上的关系，所以产量曲线与成本曲线呈现一定的对偶性，如图5-2所示。

图5-2　产量曲线与成本曲线的关系

（1）总产量曲线（TPL）与总成本曲线（TC）。TPL先递增增长再递减增长，对应TC先递减增长再递增增长。

（2）劳动平均产量曲线（APL）与平均变动成本曲线（AVC）。APL先增后减，对应AVC先减后增；APL最高点对应AVC最低点。

（3）边际产量曲线（MPL）与边际成本曲线（MC）。MPL先增后减，对应MC先减后增；MPL最高点对应MC最低点。