无风险资产及其特点，最优风险组合的选择

（一）无风险资产及其特点

1.无风险资产的定义

从资产带来的收入是否稳定这一角度可将资产分为风险资产和无风险资产。风险资产带来的货币收入具有一定的随机性，是不稳定的，而无风险资产是相对意义上的，收入是确定的，没有任何风险。

2.无风险资产的特点

无风险资产具有以下主要特征：

（1）无风险资产的收益是确定的，不存在任何变动，因而其收益变动方差为0；

（2）无风险资产的收益称为无风险收益率，一般记为rf，是一个极为重要的参数，每一个风险资产的收益均可以将其分割为两部分：无风险收益和风险溢价。风险越大，风险溢价越大，所以无风险资产的收益一般低于风险资产；

（3）无风险资产的收益和其他风险资产的收益之间不存在相关关系；

（4）现实生活中并不存在绝对意义上的无风险资产，严格地讲只有到期日与投资期相等的国债才是无风险资产。但在现实中，为方便起见，人们常将1年期的国库券或者货币市场基金当作无风险资产。

（二）带有一种无风险资产的两种资产组合

为了考察无风险资产对有效集的影响，我们首先要分析一种无风险资产和一种风险资产组成的投资组合的预期收益率和风险。

假设风险资产和无风险资产在投资组合中所占的比例分别为x1和x2，并且x1＋x2＝1，它们的预期收益分别为r1和rf，它们的标准差分别为σ1和σ2，它们之间的协方差为σ2和Cov12都为0。

1.预期收益率

由以上已知条件知道，组合预期收益率为

2.方差和标准差

根据方差计算公式，组合的风险（方差）为

标准差为

【例3－4－5】　一种风险资产是预期回报率为18%和标准差为28%的某基金，短期国债利率为8%。若投资者决定将其资产组合的70%投入到基金中，另外30%投入到货币市场的短期国库券基金中，则该资产组合的预期收益率与标准差各是多少？

（1）组合预期收益＝0．7×18%＋0．3×8%＝15%

（2）组合风险：σ2P＝（0．7×28%）2＋（0．3×0）2＋2×0×0．3×0．7＝（19．6%）2 σP＝19．6%

（三）最优风险组合的选择

1．投资与无风险资产的有效边界

（1）资本配置线

由于r1、rf和σ1已知式（3－4－12）是线性函数，其中为单位风险报酬，又称夏普比率（Sharp's Ratio）。将这种关系绘制在收益—标准差的图中，我们可以得到下图：

图3－4－10中A点表示无风险资产，B点表示风险资产，这条直线的斜率为，根据风险资产的预期收益和风险的变化而变化。

这条直线叫做资本配置线（Capital Allocation Line，CAL），它表示投资者的所有可行的风险收益组合。它的斜率等于选择的资产组合每增加一单位标准差上升的期望收益，换句话说，就是每单位额外风险的额外收益的测度。基于这一原因，该斜率也可被称为报酬与波动性比率（Reward－to－Variability Ratio）。

图3-4-10　无风险资产和风险资产组合

图3-4-11　最优风险资产组合

（2）投资与无风险资产（贷款）的有效边界

引入无风险贷款后，有效边界将发生重大变化。在图3－4－11中，弧线CD代表马科维茨有效边界，A点表示无风险资产，A点和有效边界上任意一点B相连就可以得到一条资本配置线。我们可以在马科维茨有效边界中找到一点M，使AM直线与弧线CD相切于M点。M点所代表的组合称为切点处投资组合。

因为没有任何一种风险资产或风险资产组合与无风险资产构成的投资组合可以位于AM线段的左上方。换句话说，AM线段的斜率最大，因此M点代表的组合被称为最优风险组合

在现实生活中，投资者可以借入资金并用于购买风险资产。由于借款必须支付利息，而利率是已知的。在该借款本息偿还上不存在不确定性。因此我们把这种借款称为无风险借款。

为了分析方便起见，我们假定投资者可按相同的利率进行无风险借贷。

①无风险借款并投资于一种风险资产的情形

为了考察无风险借款对有效集的影响，我们首先分析投资者进行无风险借款并投资于一种风险资产的情形。为此，我们只要对上面的推导过程进行适当扩展即可。

我们可以把无风险借款看成负的投资，则投资组合中风险资产和无风险借款的比例也可用X1和X2表示，且X1＋X2＝1，X1＞1，X2＜0。这样，在图上表现为AB线段向右边的延长线上，如图3－4－13所示。这个延长线再次大大扩展了可行集的范围。

图3-4-13　引入无风险借款后可行集的扩展

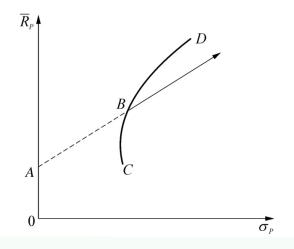
图3-4-14　无风险资产和风险资产组合的组合

②无风险借款并投资于风险资产组合的情形

同样，由无风险借款和风险资产组合构成的投资组合，其预期收益率和风险的关系与由无风险借款和一种风险资产构成的投资组合相似。

我们假设风险资产组合B是由两种风险证券组成的，则由风险资产组合B和无风险借款A构成的投资组合的预期收益率和标准差一定落在AB线段向右边的延长线上，如图3－4－14所示。

（2）无风险借款对有效集的影响

引入无风险借款后，有效集也将发生重大变化。在图3－4－15中，弧线CD仍代表马科维茨有效集，M点仍表示CD弧线与过A点直线的相切点。在允许无风险借款的情形下，投资者可以通过无风险借款并投资于最优风险资产组合M，使有效集由MD弧线变成AM线段向右边的延长线。这样，在允许无风险借贷的情况下，马科维茨有效集由CMD弧线变成过A、M点的直线在M点右边的部分。图中虚线部分代表允许投资无风险资产的情况。

（3）无风险借款对投资组合选择的影响

对于不同的投资者而言，允许无风险借款对他们的投资组合选择的影响也不同。

对于厌恶风险程度较轻的投资者，他将选择其无差异曲线与AM直线切点所代表的投资组合。如图3－4－16（a）所示。

对于较厌恶风险从而其选择的投资组合位于CM弧线上的投资者而言，如图3－14－16（b）所示，他只会用自有资产投资于风险资产，而不会进行无风险借款。

图3-4-15　允许无风险借款后的有效集

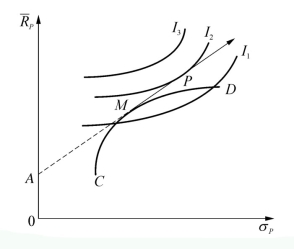
图3-4-16（a）　风险厌恶程度轻的投资者最佳组合

图3-4-16（b）　风险厌恶程度高的投资者最佳组合

图3-4-17　允许无风险借贷后的有效集

4.风险和期望收益的杠杆效应

一般而言，两者的关系可以概括为：高风险要求高的期望收益。

5.含有无风险的贷和借的有效边界

在允许无风险借贷的情况下，有效边界变成一条直线，该直线经过无风险资产A点并与马科维茨有效边界相切，CM和MD曲线都不再是有效的。我们同样可以从图3－4－17理解：

若最优投资组合位于M点左侧，说明投资者风险厌恶程度较高，会将一部分资产投资到无风险资产；若最优投资组合位于M点右侧，说明投资者风险厌恶程度较低，会借入无风险资产和自有资产并一起投资于风险资产。

（四）投资者效用和无风险资产

1.市场组合

根据分离定理（见2），我们可以得到另一个重要结论：在均衡状态下，每种证券在均点处投资组合中都有一个非零的比例。

这是因为，根据分离定理，每个投资者都持有相同的最优风险组合（M）。如果某种证券在M组合中的比例为零，那么就没有人购买该证券，该证券的价格就会下降，从而使该证券预期收益率上升，一直到在最终的最优风险组合M中该证券的比例非零为止。

同样，如果投资者对某种证券的需要量超过其供给量，则该证券的价格将上升，导致其预期收益率下降，从而降低其吸引力，它在最优风险组合中的比例也将下降，直至对其需求量等于其供给量为止。

因此，在均衡状态下，每一个投资者对每一种证券都愿意持有一定的数量，市场上各种证券的价格都处于使该证券的供求相等的水平上，无风险利率的水平也正好使得借入资金的总量等于贷出资金的总量。这样，在均衡时，最优风险组合中各证券的构成比例等于市场组合（Market Portfolio）中各证券的构成比例。所谓市场组合是指由所有证券构成的组合，在这个组合中，每一种证券的构成比例等于该证券的相对市值。一种证券的相对市值等于该证券总市值除以所有证券的市值的总和。

习惯上，人们将切点处组合叫做市场组合，并用M来表示。从理论上说，M不仅由普通股构成，还包括优先股、债券、房地产等其他资产。但在现实中，人们常将M局限于普通股。

【复习提示及知识补充】

复习时我们一定要注意所谓“市场组合”的特征，总结起来有以下几点供大家参考：

（1）市场组合是一种理想状态，由市场上所有存在的风险资产组成，各种风险资产所占比例都不可能为零，每种证券所占比例由其相对市值决定；

（2）市场组合代表的是一种市场动态均衡状态，在市场组合中每一种证券的供求都处于动态均衡中；

（3）市场组合是一种将非系统性风险完全分散的组合，即代表最优风险资产组合点，其贝塔值为1，可以用市场组合风险来代表不可分散风险即市场风险的大小。

其中第三条很重要，大家可以结合这一点来思考一下，在CML公式中市场组合收益和方差的含义。

2.分离定理

（1）资本资产定价理论的假定

为了推导资本资产定价模型，有以下假定：

①所有投资者的投资期限均相同。

②投资者根据投资组合在单一投资期内的预期收益率和标准差来评价这些投资组合。

③投资者永不满足，当面临其他条件相同的两种选择时，他们将选择具有较高预期收益率的那一种。

④投资者是厌恶风险的，当面临其他条件相同的两种选择时，他们将选择具有较小标准差的那一种。

⑤每种资产都是无限可分的。

⑥投资者可按相同的无风险利率借入或贷出资金。

⑦税收和交易费用均忽略不计。

⑧对于所有投资者来说，信息都是免费的并且是立即可得的。

⑨投资者对于各种资产的收益率、标准差、协方差等具有相同的预期。

这些假定虽然与现实世界存在很大差距，但通过这个假想的世界，我们可以导出证券市场均衡关系的基本性质，并以此为基础，探讨现实世界中风险和收益之间的关系。

（2）分离定理

在上述假定的基础上，我们可以得出如下结论：

①根据相同预期的假定，我们可以推导出每个投资者的切点处投资组合（最优风险组合）都是相同的（如图3－4－17中的M点），从而每个投资者的线性有效集都是一样的。

②由于投资者风险—收益偏好不同，其无差异曲线的斜率不同，因此他们的最优投资组合也不同。

由此我们可以导出著名的分离定理：

投资者对风险和收益的偏好状况与该投资者风险资产组合的最优构成是无关的。

（五）资本市场线及其斜率和预期收益的计算

按资本资产定价模型的假设，我们就可以很容易地找出有效组合风险和收益之间的关系。如果我们用M代表市场组合，用Rf代表无风险利率，从Rf出发画一条经过M的直线，这条线就是在允许无风险借贷情况下的线性有效集，在此我们称为资本市场线（Capital Market Line），如图3－4－18所示。任何不利用市场组合以及不进行无风险借贷的其他所有组合都将位于资本市场线的下方。

图3418　资本市场线

从图3－4－18可以看出，资本市场线的斜率等于市场组合预期收益率与无风险证券收益率之差）除以它们的风险之差（σM－0），即）／σM，由于资本市场线与纵轴的截距为Rf，因此其表达式为：

其中和σP分别代表最优投资组合（即市场组合）的预期收益率和标准差。

从式（3－4－13）可以看出，证券市场的均衡可用两个关键数字来表示：一是无风险利率（Rf），二是单位风险报酬－Rf）／σM］，它们分别代表时间报酬和风险报酬。因此，从本质上说，证券市场提供了时间和风险进行交易的场所，其价格则由供求双方的力量来决定。

【复习提示及知识补充】

CAL和CML线的异同比较

资本配置线和资本市场线都是表示将投资在无风险资产和风险资产之间分配的曲线。不同的是，CML是一条特殊的资本配置线，其风险资产是市场组合（最优风险资产组合），所以通过M点，而CAL有无数条，不一定通过M点。

（六）组合和单个证券的风险和预期收益

详见本部分一（三）相关内容。

（七）贝塔和单个证券的风险

证券市场线（SML）一般用于估计一种证券的预计收益，而证券特征线则用于描述一种证券的实际收益。

1.贝塔与特征线

证券特征线（SCL，Security Characteristic Line）是单个证券i的实际收益率与市场组合实际收益率间的回归直线。在以ri为纵坐标、rM为横坐标的坐标系中，回归直线方程为：ri＝αi＋rMβi，其中αi和βi为回归系数，βi称为证券i的β系数，表示证券特征线的斜率。

β系数的估计是CAPM模型实际运用时最为重要的环节之一。在实际运用中，人们常用单因素模型来估计β值。单因素模型一般可以表示为

在这里，Rit为证券i在t时刻的实际收益率，RMt为市场指数在t时刻的收益率，αi为截距项，βi为证券i收益率变化对市场指数收益率变化的敏感度指标，它衡量的是系统性风险，εit为随机误差项，该随机误差项的期望值为零。公式（3－4－14）也常被称为市场模型。

特征线是从对应于市场指数收益率的证券收益率的散点图拟合而成的。根据单因素模型的公式，β值可以看作特征线的斜率，它表示市场指数收益率变动1%时证券收益率的变动幅度。

2.特征线方程

在以ri为纵坐标、rM为横坐标的坐标系中，回归直线方程为：ri＝αi＋rMβi，其中αi和βi为回归系数，利用历史数据回归得到直线方程就是证券i的特征线方程。

3.贝塔的作用

贝塔系数（β）反映个别证券随着市场投资组合变动的趋势，用以计量个别证券相对于市场组合的变动程度。资产的定价中，那些只影响该证券的方差而不影响该股票与股票市场组合的协方差的因素在定价中不起作用，对定价唯一起作用的是该股票的β系数。

4.贝塔作为相对风险的衡量

贝塔系数指个别股票相对于市场平衡风险的变动程度，即表明股票收益对于系统风险的反应程度。这种反应是对个别股票对于市场的相对变动的衡量，和标准差衡量总体风险不同。

贝塔系数的意义主要表现在：（1）它是一种能反映各股票相对于整个股市的变动性指数，因而它可以衡量该股票的市场风险。如果某种股票的贝塔系数等于1，则表明当整个股市行情上涨10%时，该股票的行情也上涨10%；反之，若股票行情下跌10%，则该股行情也会下跌10%。（2）通过贝塔系数所反映的是与市场风险的关系、定量分析风险与报酬的关系。

（八）风险的划分

1.系统性风险

2.非系统性风险

3.总风险

系统性风险和非系统性风险之和为总风险，反映收益的整体变动情况。我们一般用标准差或者方差来衡量某一证券的总风险。标准差或者方差越大，总风险越大。

（九）一种证券的预期收益率

资本市场线反映的是有效组合的预期收益率和标准差之间的关系，任何单个风险证券由于均不是有效组合而一定位于该直线的下方。因此资本市场线并不能告诉我们单个证券的预期收益与标准差（即总风险）之间应存在怎样的关系。为此，我们有必要作进一步的分析。

1.证券市场线的含义

证券市场线的推导

由前面内容，我们可以知道市场组合标准差的计算公式为

其中：XiM和XjM分别表示证券i和j在市场组合中的比例。式（3－4－15）可以展开为

根据协方差的性质可知，证券i跟市场组合的协方差（即CoviM，这里用σiM简便表示）等于证券i跟市场组合中每种证券协方差的加权平均数：

如果我们把协方差的这个性质运用到市场组合中的每一个风险证券，并代入式（3－4－15），可得

其中：σ1　M表示证券1与市场组合的协方差，σ2　M表示证券2与市场组合的协方差，依此类推。式（3－4－17）表明，市场组合的标准差等于所有证券与市场组合协方差的加权平均数的平方根，其权数等于各种证券在市场组合中的比例。

由此可见，在考虑市场组合风险时，重要的不是各种证券自身的整体风险，而是其与市场组合的协方差。这就是说，自身风险较高的证券，并不意味着其预期收益率也应较高；同样，自身风险较低的证券，也并不意味着其预期收益率也就较低。单个证券的预期收益率水平应取决于其与市场组合的协方差。

由此我们可以得出如下结论：具有较大σiM值的证券必须按比例提供较大的预期收益率以吸引投资者。由于市场组合的预期收益率和标准差分别是各种证券预期收益和各种证券与市场组合的协方差（σiM）的加权平均数，其权数均等于各种证券在市场组合中的比例，因此如果某种证券的预期收益率相对于其σiM值太低的话，投资者只要把这种证券从其投资组合中剔除就可提高其投资组合的预期收益率，从而导致证券市场失衡。同样，如果某种证券的预期收益率相对于其σiM值太高的话，投资者只要增持这种证券就可提高其投资组合的预期收益率，从而也将导致证券市场失衡。在均衡状态下，单个证券风险和收益的关系可以写为

式（3－4－18）所表达的就是著名的证券市场线（Security Market Line），它反映了单个证券与市场组合的协方差和其预期收益率之间的均衡关系。如果我们用作纵坐标，用σiM作横坐标，则证券市场线在图上就是一条截距为Rf、斜率为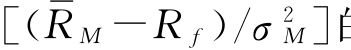的直线，如图3－4－19（a）所示。

从式（3－4－18）可以有趣地发现，对于σiM等于0的风险证券而言，其预期收益率应等于无风险利率，因为这个风险资产跟无风险资产一样，对市场组合的风险没有任何影响。更有趣的是，当某种证券的σiM＜0时，该证券的预期收益率甚至将低于Rf。

把式（3－4－17）代入式（3－4－18），我们有

其中：βiM称为证券i的β系数，它是表示证券i与市场组合协方差的另一种方式。式（3－4－19）是证券市场线的另一种表达方式。如果我们用为纵轴，用βiM为横轴，则证券市场线也可表示为截距为Rf、斜率为）的直线，如图3－4－19（b）所示。

β系数的一个重要特征是，一个证券组合的β值等于该组合中各种证券β值的加权平均数，权数为各种证券在该组合中所占的比例，即：

其中：βpM表示组合P的β值。

由于任何组合的预期收益率和β值都等于该组合中各个证券预期收益率和β值的加权平均数，其权数也都等于各个证券在该组合中所占比例，因此，既然每一种证券都落在证券市场线上，那么由这些证券构成的证券组合也一定落在证券市场线上。

比较资本市场线和证券市场线可以看出，只有最优投资组合才落在资本市场线上，其他组合和证券则落在资本市场线下方。而对于证券市场线来说，无论是有效组合还是非有效组合，它们都落在证券市场线上。

既然证券市场线包括了所有证券和所有组合，因此也一定包含市场组合和无风险资产。在市场组合那一点，β值为1，预期收益率为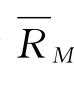，因此其坐标为（1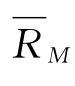）。在无风险资产那一点，β值为0，预期收益率为Rf，因此其坐标为（0，Rf）。证券市场线反映了在不同的β值水平下，各种证券及证券组合应有的预期收益率水平，从而反映了各种证券和证券组合系统性风险与预期收益率的均衡关系。由于预期收益率与证券价格与反比，因此证券市场线实际上也给出了风险资产的定价公式。

资本资产定价模型所揭示的投资收益与风险的函数关系，是通过投资者对持有证券数量的调整并引起证券价格的变化而达到的。根据每一证券的收益和风险特征，给定一证券组合，如果投资者愿意持有的某一证券的数量不等于已拥有的数量，投资者就会通过买进或卖出证券进行调整，并因此对这种证券价格产生涨或跌的压力。在得到一组新的价格后，投资者将重新估计对各种证券的需求，这一过程将持续到投资者对每一种证券愿意持有的数量等于已持有的数量，证券市场达到均衡。

图3-4-19　证券市场线

2.证券市场线方程与计算

证券市场线一般表达式和常用表达式：

一般表达式：

常用表达式。常用表达式常常会考到相应的计算，我们可以通过一道例题来理解。

【例3－4－6】　在1997年，短期国库券（被认为是无风险的）的收益率约为5%。假定一贝塔值为1的资产组合市场要求的期望收益率是12%，根据资本资产定价模型（证券市场线）：

（1）市场资产组合的预期收益率是多少？

因为市场组合的定义为1，它的预期收益率为12%。

（2）贝塔值为0的股票的预期收益率是多少？

β＝0意味着无系统风险。因此，资产组合的公平的收益率是无风险利率，为5%。

（3）假定投资者正考虑买入一股股票，价格为40美元。该股票预计来年派发红利3美元。投资者预期可以以41美元卖出。股票风险β＝－0.5，该股票是高估还是低估了？

运用证券市场线，β＝－0.5的股票公平收益率为

E（ri）＝rf＋（rM－rf）β＝5%＋（12%－5%）（－0.5）＝1.5%

利用第二年的红利和资本利得计算预期收益为

因为预期收益超过了公平收益，股价被低估了。

（十）证券市场线与资本市场线的区别

只有最优投资组合才落在资本市场线上，其他组合和证券则落在资本市场线的下方；而对于证券市场线而言，无论是有效组合还是非有效组合，它们都落在证券市场线上。

1.相同点

（1）理论基础相同：都是以马科维茨投资组合理论为分析基础的；

（2）前提假设相同：具有相同的假设前提，证券市场有效性、投资者对收益率的不满足性、投资者基于收益率、风险（期望值、方差）分析；

（3）SML可由CML推导出来。

2.不同点

（1）表达式不同

资本市场线表达式：

证券市场线的两种表达式：

（2）坐标轴不同

资本市场线横轴表示投资组合的风险σp，纵轴表示投资组合的预期收益；证券市场线横轴表示证券i与市场组合的协方差σiM或β值，纵轴表示证券i的预期收益

（3）含义不同

资本市场线描述了有效投资组合风险与预期收益之间的关系，而证券市场线界定的风险与收益的关系适用于所有的资产和组合，无论其有效与否。因此，资本市场线上的所有组合对应点一定在证券市场线上，而非有效组合的对应点也将落在证券市场线上，但是在资本市场线以下。

【复习提示及知识补充一】

为了方便大家记忆，我们可以整理成一个表格来表示两者关系：