光线经过大质量恒星

5．宇宙的尺度

日、月、行星以及恒星距离我们有多远？这个重要而困难的问题，自古以来就引起了人们的注意。远在公元前3世纪古希腊阿里斯塔克就用严格的几何方法推算出了日、月与地球的距离之比以及日月与地球的大小之比，他测得月亮上弦时日月之间的角距离为87°，从而算出月地距离与日地距离之比为1/20，此数值虽不准确，却是人类第一次空间距离测定。公元前2世纪，喜帕恰斯求得地月距离为地球直径为30·2倍。1751—1753年法国科学家首次用三角测量法精确测定了月球距离。图2-7上显示了用三角测量法测量遥远天体距离的方法原理。设我们从基线AB上观察遥远的天体M，可以测量出有一个视差角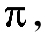设可用角秒来表示，容易给出计算天体到我们的距离的公式为

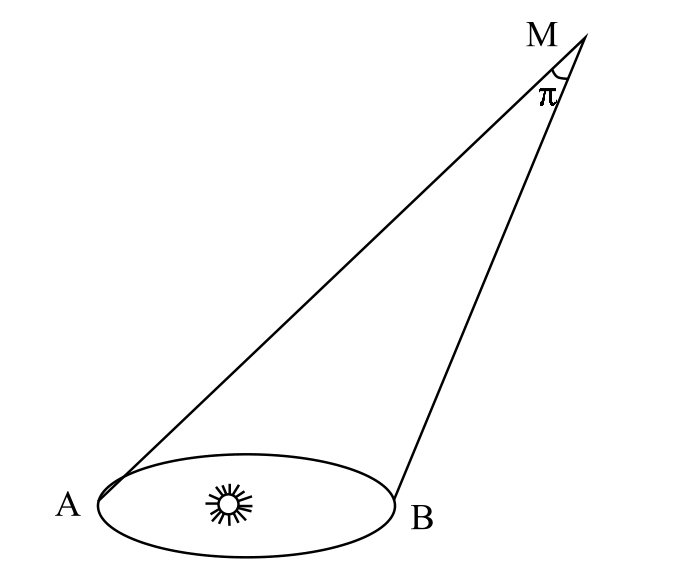
图2-7　用视差法测量天体的距离

在测量太阳系内天体的距离时，常常取α等于地球半径，以便作统一归算，这样求得之视差被称为周日地平视差。月亮的周日地平视差57′，是所有天体中最大的，太阳的视差等于8.80″。太阳离我们的距离比月亮远约400倍。

1672年法国天文家卡西尼根据在巴黎和法属圭亚那的观测测定了火星视差。根据开普勒行星运行第三定律，只要知道了任意一颗行星到我们的距离，便可以推算出地球到太阳的距离，以及所有行星到太阳的距离。以后又发展了用观测小行星测定太阳系天体距离的方法。在第二次世界大战之后，采用雷达波直接测定火星、金星及其他天体到地球的距离，测量精度已达几米。

测量恒星到地球的距离必须依靠地球的轨道运动。利用相隔半年的二次观测，地球正好分别处于地球轨道的两边，离我们比较近的恒星由于周年视差会在较远的暗弱的恒星背景上显示出一个偏离，测量出这个偏离，就可以算出恒星离我们的距离。由于恒星离我们非常远，直到1837—1839年，才分别由俄国的斯特鲁维、德国的白塞耳和英国的享德森分别测得了织女星（天琴α）、天鹅61和南门二（半人马α）三颗恒星的周年视差。斯特鲁维测定的织女星的周年视差为0.12″，它相当于将我国一角硬币放在38km远处所看到的角度，由此可见测定恒星视差工作之困难。由织女星的周年视差可以算出织女星离我们有27光年。恒星离我们的距离大大超出了古代科学家对宇宙的想象。距离我们最近的恒星是南门二的伴星比邻星，距离为4.22光年。到20世纪中已测定了上千颗恒星的周年视差。

以三角测量法得到的大量恒星周年视差作为基础，发展了许多种测量遥远天体距离的方法，以下列举几种主要的方法。

（1）利用造父变星

这一类周期性脉动变星，其变化原因是因为它们在不停地收缩和扩张，像心脏一样脉动。变光周期为1～50天，光变幅度从0.1～2个星等。其中最典型的是仙王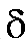（造父一）。经过大量观测表明，造父变星的平均光度与变光周期之间存在着密切关系，即只要知道造父变星的周期，就可以知道造父变星的绝对亮度，利用这个关系我们可以测定非常遥远的天体的距离，只要在星团或星云中观测到造父变星，测定造父变星的变光周期和星等，即可以算出造父变星所在星团或星云离我们的距离，因此造父变星又有“量天尺”之称。

利用造父变星测出我们银河系的两个伴星系，大麦哲伦星云和小麦哲伦星云离我们的距离分别是16万光年和19万光年，离我们最近的仙女座大星云距离我们约200万光年。

（2）利用天琴座RR型变星

这类变星的变光周期尽管不同，但绝对星等都在0.5等左右，因此可根据RR型变星的亮度计算天体的距离。

（3）利用赫罗图

关于赫罗图的问题，我们将在星空巡礼一章予以介绍。这种方法是利用处在主星序上的星，其色指数与绝对星等有着很好的关系。因此，根据色指数可知恒星的绝对星等，再由恒星星等可以算出恒星到我们的距离。

（4）利用谱线红移

观测表明，河外星系都有谱线红移现象，而且红移量同星系的距离成正比。因此根据红移量可估算星系的距离。

此外，还可以根据恒星的运动、新星和超新星的变化特征、星团内恒星的特征分布以及双星的运动等估算天体的距离。