【摘要】:5.2.3 解析内插法1.线性插值当待插值点与周围相邻的两个测量点在一条直线上时,可以采用线性插值的方法得到插值点的近似值。距离加权平均法较为常用。还有一些比较适用的方法,如趋势面拟合法等。
解析内插法_地球物理基础综合
5.2.3 解析内插法
1.线性插值
当待插值点与周围相邻的两个测量点在一条直线上时,可以采用线性插值的方法得到插值点的近似值。设与待插值点相邻的两个点的坐标与观测值为(xi,yi,gi)(i=1,2),则待插值点(x,y)处的近似计算值g为:
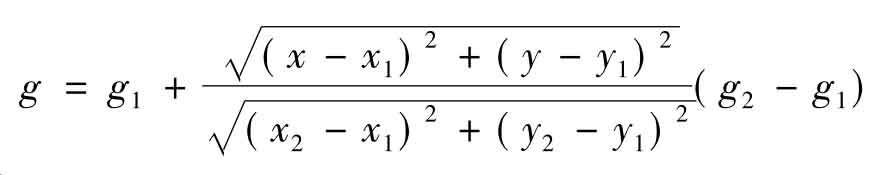
利用上式即可利用已知的两测点求得待定点的重力值。
2.距离加权平均法(此处利用网络节点值插值非节点处重力值)
插值方法不改变原始数据点的值,而是根据原始数据点值来插补空白区的值,因此当数据分布较为均匀时有很高的逼近程度。距离加权平均法较为常用。设待插值点(xi,yi)至网络节点(xj,yj)的距离dij,那么在网络中,待插值点(xi,yi)处的内插值可以表示为:
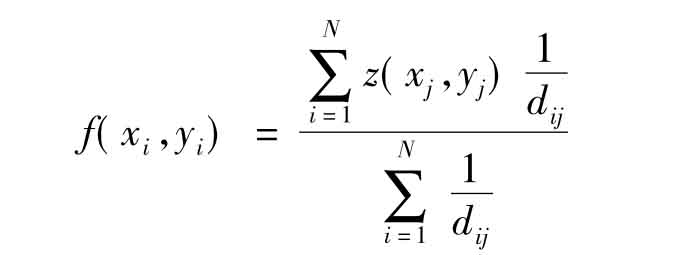
当dij=0时f(xi,yi)=z(xj,yj)。
3.其他插值方法
以上介绍的插值方法是在二维平面进行(当然也可以用于一维),这里再简单列举几种本文用到的在单个测线上用到的一维插值方法,包括拉格朗日多项式插值、三次样条插值以及三次多项式插值。还有一些比较适用的方法,如趋势面拟合法等。
![]()
采用适当的线性方程组的求解方法可以得到系数矩阵A。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















