干旱指标选取及干旱等级划分

干旱指标选取及干旱等级划分_塔河流域干旱预警

6　塔河流域干旱灾害风险评估与区划

干旱是指因降水异常减少、蒸发增大，或入境水量不足，造成城乡居民生活、工农业生产以及生态环境等正常用水需求得不到满足的现象。从不同的关注角度看，干旱可以划分为气象干旱、水文干旱、农业干旱和社会经济干旱四种干旱类型。与干旱类型相对应，干旱识别指标大致也可以分为四类。

气象干旱是由于收入项降水的异常短缺或由于支出项蒸散发的异常增大形成。因降水是主要的收入项，气象干旱通常以降水量的短缺程度作为干旱强度识别的指标。常见的气象干旱指标有：标准化降水指标、降雨量距平百分率、降雨量标准差、PDSI指标、Z指标、P指标、降水温度均一化指标、Bhalme－Mooley干旱指标、综合气象干旱指数等。水文干旱侧重地表或地下水水量的短缺，Linsley等（1975）把水文干旱定义为：“某一给定的水资源管理系统下，河川径流在一定时期内满足不了供水需要”。如果在一段时期内，流量持续低于某一特定的阀值，则认为发生了水文干旱，阀值的选择可以依据流量的变化特征，或者根据水需求量来确定。农业干旱是指在农作物生长发育过程中，因降水不足、土壤含水量过低和作物得不到适时适量的灌溉，致使供水不能满足农作物的正常需水，而造成农作物减产。体现干旱程度的主要因子有：降水、土壤含水量、土壤质地、气温、作物品种和产量，以及干旱发生的季节等。社会经济干旱指由于经济、社会的发展，需水量日益增加，以水分影响生产、消费活动等来描述的干旱。其指标常与一些经济商品的供需联系在一起，如与建立降水、径流和粮食生产、发电量、航运、旅游效益以及生命财产损失等有关。社会经济干旱指标：社会经济干旱指标主要评估由于干旱所造成的经济损失。通常拟用损失系数法，即认为航运、旅游、发电等损失系数与受旱时间、受旱天数、受旱强度等诸因素存在一种函数关系。虽然各类干旱指标可以相互借鉴引用，但其结果并非能全面反映各学科干旱问题，要根据研究的对象选择适当的指标。

虽然四种干旱定义和干旱识别指标均不一样，但也存在一定的联系。干旱的表现形式都是可供水资源量满足不了生活、生产或生态的需要，导致原因均是降水或过境水量的异常减少或蒸散发的异常增大。降水是水资源的主要来源，蒸发是水资源的主要损失形式，直接影响着河川径流、土壤含水量的多少以及作物、人类社会和生态环境对水资源需求的满足程度。因此，气象干旱可以理解为前因型定义，而其他的干旱是水资源短缺在各自领域内的反映，属于后果型定义，正是由于有气象干旱出现才可能有其他干旱的出现。本研究从气候干旱和农业干旱的角度出发，分别对塔河流域的气象干旱和农业干旱风险进行评估，并找出两者之间的关系。

6．1　基于SPI的气象干旱风险评估

塔河流域区别于其他区域的一个最重要的特点是其县级行政区划中包括山区、戈壁滩和沙漠等无人区，无经济活动的区域则不存在旱灾易发问题，因此风险区划图应该按照县级行政区划中的绿洲范围进行绘制，并与兵团所在区域范围在制图中进行了拼接，避免了地方系统与兵团系统边界相互嵌套的问题。国内外研究风险评估的方法很多，尽管新疆的干旱也受径流量的影响，鉴于掌握和搜集到的基础资料和前面研究的降雨量能很好地反映塔河干旱事件。本研究利用不同尺度下的标准降雨指数作为风险区划的备选指标。

6．1．1　标准降水指数

标准降水指标由Mckee等在1993年提出，从不同时间尺度评价干旱。由于标准降水指标具有资料获取容易，计算简单，能够在不同地方进行干旱程度对比等优点，因而得到广泛应用。假定计算时间尺度为m的标准降水指标（通常m取1，3，6，12，24等），先将日降水量处理为月降水资料，依次对连续m个月的月降水资料求和，得到m个月累积降水序列。由于年内不同月份之间的自相关性可能会导致分布函数拟合时出现误差，为消除样本的自相关性，在累积降水序列中，将时间序列中不同月份的SPI值分别先进行计算，再合起来得到整个时间序列的SPI值。也就是将累积降水序列按不同月份分类得到一个序列，例如计算3月份的SPI值则选取整个时间序列中3月份的值，然后对该序列采用Gamma分布对其配线，配线完成后，计算累积降水的累积概率，再通过标准正态分布反函数转换为标准正态分布，所得结果即是该月份的标准降水指标值，以此类推从而得到所有月份的SPI值，将这些不同月份的SPI值合并起来，则得到整个序列的SPI值。

设X表示月降水时间序列，Xw表示w时间尺度的累积月降水序列，其中，w＝1，3，6，…，Xmwon， 表示某月份对应的w时间尺度的累积月降水序列，其中mon表示月份，mon＝1，2，3，…，12，依次表示1～12月。例如X86表示6个月时间尺度的3～8月的累积降水序列。SPI计算公式为：

式中：F——Gamma分布函数；

φ－1——标准正态分布的反函数。

由于标准降水指标基于标准正态分布，因此不同等级标准降水指标干旱具有对应的理论发生概率，其等于特定干旱等级中标准降水指标上下限值的标准正态分布累积概率之差。标准降水指标值对应的干旱等级及发生概率见表6．1。

表6．1　标准降水指标干旱等级

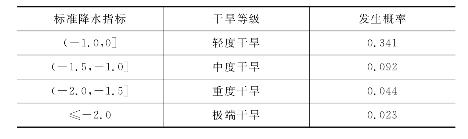
由于干旱受前期降水的影响，因而标准降水指标考虑不同时间尺度的值，将不同时间尺度的前期降水纳入计算，考虑它们对水资源盈缺状况的影响。不同时间尺度的标准降水指标具有不同的物理意义。时间尺度较短的标准降水指标能一定程度反映短期土壤水分的变化，这对于农业生产是有重要意义的。时间尺度较长的标准降水指标能反映较长时间的径流量变化情况，对于水库管理有重要作用。短期干旱导致土壤表层水分缺失，这对于农业耕作具有重大的负面影响，农作物不能获取足够的水分，引起农业干旱。

6．1．2　干旱指标选取及干旱等级划分

本文的SPI的时间尺度分别选择3个月、6个月、9个月和12个月，利用风险概率方法将不同尺度的不同等级的干旱通过采用GIS统计分析和叠加分析的功能，并利用1990—2007年塔河各县市的干旱受灾面积、成灾面积、绝收面积分别占耕地面积的比重以及单位公顷损失粮食（万斤）四个指标作为选择风险区划图的参考指标，见表6．2和图6．1、图6．2。从表图可知，和田地区的县市、巴州的若羌县和阿克苏地区的乌什县、阿瓦提县的旱灾受灾面积比重大于其他地州/地区的县市的旱灾受灾面积，阿克苏地区的阿克苏市的旱灾受灾面积比重最小，见图6．1。旱灾成灾面积的比重变化基本与成灾面积的变化相似，但是除阿克苏市以外阿克苏地区、和田地区、巴州的各县市成灾面积比重大于克州和喀什地区，见图6．2。成灾率（受灾面积与成灾面积比值）巴州的成灾率98%为各地区最大，意味着巴州地区干旱都会成灾害；其次是和田地区的80．0%，克州的69．3%，阿克苏的65．4%，喀什的成灾率28．64%是塔河流域各地州最低的。阿克苏地区的阿瓦提县绝收面积所占比重最大，其次是和田地区的皮山县、墨玉县，阿克苏地区的库车县、克州的阿图什市、阿克陶县、阿合奇县。而和田地区的和田市是绝收面积比重最小的，其次是阿克苏地区的沙雅县、巴州的尉犁县和喀什地区，见图6．3。阿克苏地区的库车县、沙雅县、拜城县，喀什地区的莎车县、叶城县和和田地区的墨玉县、皮山县是单位公顷损失粮食最多的县市；克州的乌恰县、阿合奇县，喀什地区的喀什市、塔什库尔干县和阿克苏地区的柯坪县是单位公顷粮食损失最小的区域，见图6．4、表6．2。

从各地州/地区的干旱受灾面积趋势图6．5可知，喀什地区平均旱灾受灾面积最大，但是受灾面积有减小的趋势；其他四个地州/地区的旱灾受灾面积呈增加的趋势，和田地区的旱灾受灾面积增加趋势最明显，而且各地州/地区的旱灾受灾面积从1990年开始增加的比较明显，尽管1995年以后国家加大了对于抗旱浇灌的能力，见图6．6，但并没有减缓旱灾受灾面积的增加。各地州/地区的旱灾受灾面积的趋势变化基本与图6．1～图6．4反映的旱灾情况相同。结合塔河流域各县（市）的干旱受灾面积、成灾面积、绝收面积分别占耕地面积的比重以及单位公顷损失粮食（万斤）四个指标，并且对比不同尺度不同等级SPI的干旱风险，可以看出12个月尺度的SPI在反映塔河流域干旱情况方面优于其他尺度SPI，12个月尺度的SPI风险见图6．7。

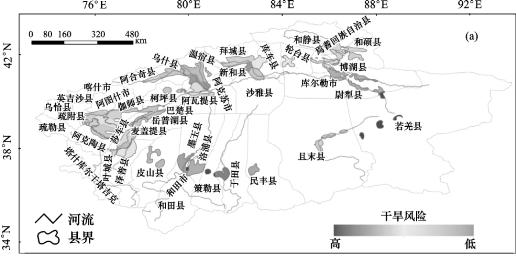
图6．1　塔河流域各县（市）单位干旱受灾面积占耕地面积比重

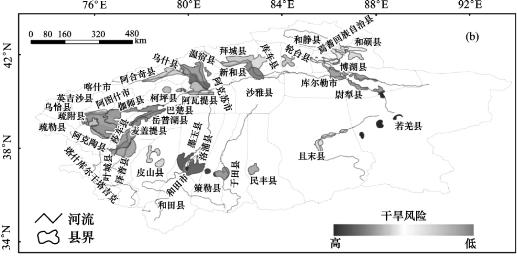
图6．2　塔河流域各县（市）单位成灾面积占耕地面积比重

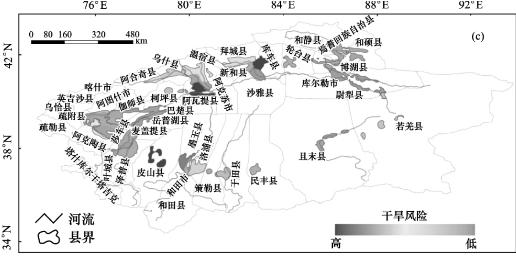
图6．3　塔河流域各县（市）干旱绝收面积占耕地面积比重

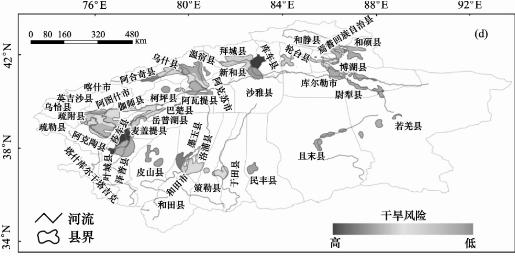
图6．4　塔河流域各县（市）风险区划图指标

表6．2　塔河流域各县（市）单位公顷粮食损失

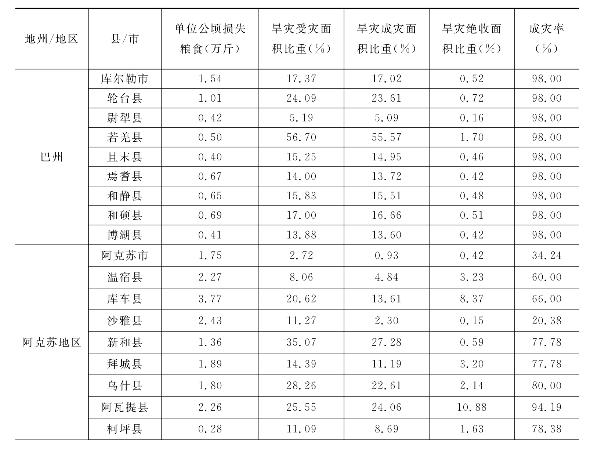
续表6．2

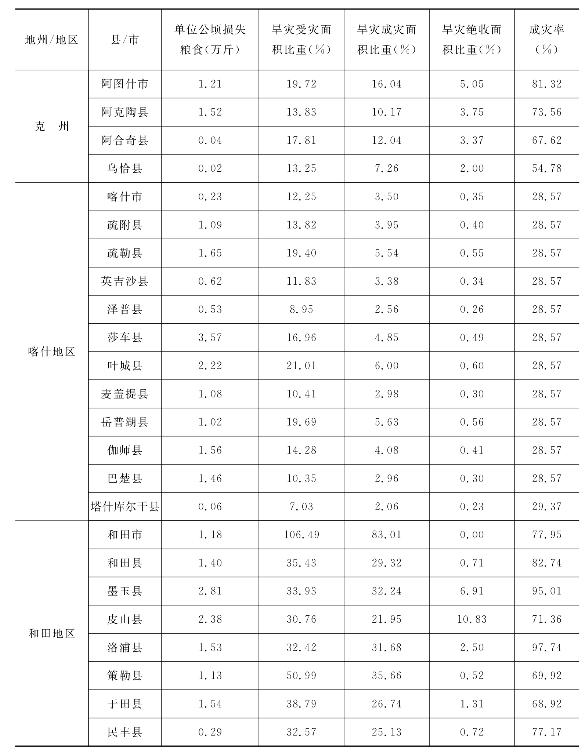
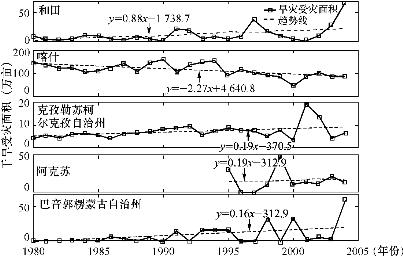
图6．5　塔河流域各地县（市）干旱受灾面积及趋势

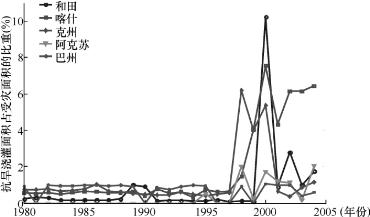
图6．6　抗旱浇灌面积占受灾面积的比重

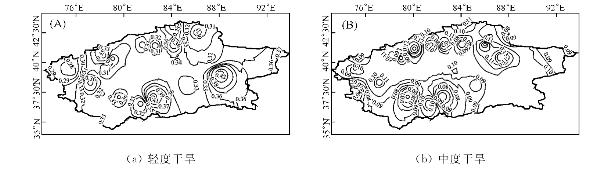
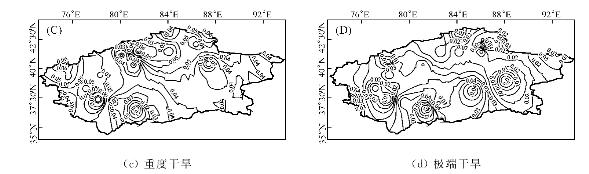
图6．7　干旱发生概率空间分布

由图6．8知，塔河流域的羌县、轮台县、民丰县、和田市、墨玉县、莎车县和泽普县的轻度干旱发生的频率高，而克州和巴州的开都－孔雀河流域的县市、阿克苏河流域的县市轻度干旱发生的频率低。

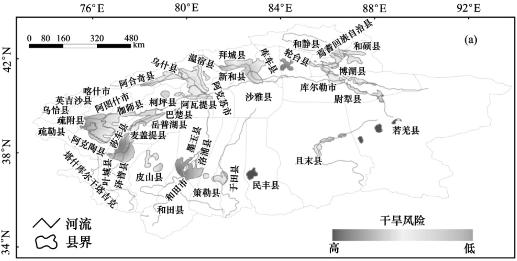
图6．8（彩插7）　轻度干旱发生概率空间分布

图6．9显示阿克苏流域、开都－孔雀河流域和塔河下游的县市发生中度干旱频率最高，其次是渭干河流域，而和田地区中度干旱的频率却是最低的。

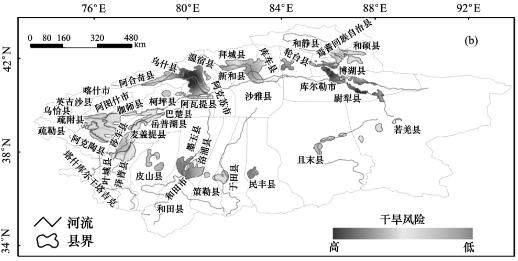
图6．9（彩插8）　中度干旱发生概率空间分布

图6．10中严重干旱发生频率高的地区主要有渭干河流域的县市和叶尔羌河流域的县市，和田河和阿克苏河流域发生严重干旱的频率较低。但是和田河流域县市和巴州的若羌等县极端干旱发生频率高，其次是克州和阿克苏地区的县市，渭干河流域和喀什地区的极端干旱发生频率较低。

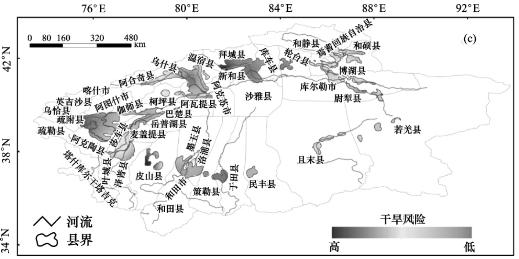
图6．10（彩插9）　重度干旱发生概率空间分布

由图6．11知，塔河流域昆仑山北坡轻度、极端干旱发生频率大于天山南坡地区，旱灾受灾面积和成灾面积占耕地面积的比重也高于天山南坡地区，而且和田河等昆仑山北麓河流干旱发生程度也是南疆地区最严重的，这与和田河流域的渠道渗透率、现状供水率等抗旱措施远低于其他流域有重要关系。

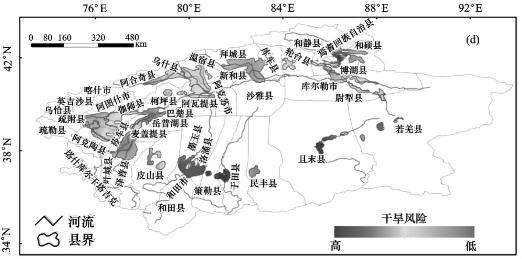
图6．11（彩插10）　极端干旱发生概率空间分布

6．2　基于可变模糊评价法的农业干旱风险评估

陈守煜教授建立的可变模糊集理论与方法是工程模糊集理论与方法的进一步发展，作为其核心的相对隶属函数、相对差异函数与模糊可变集合的概念与定义是描述事物量变、质变时的数学语言和量化工具。

6．2．1　可变模糊集定义

定义：设论域U上的对立模糊概念（事物、现象）以A和Ac表示吸引性质与排斥性质，对U中的任意元素u，u∈U，在参考连续统区间［1，0］（对A）与［0，1］（对Ac）任一点上，吸引与排斥性质的相对隶属度分别为μA（u）、μAc（u）。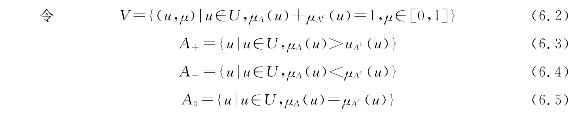

设C是可变因子集，

（6．2）～（6．10）式称为以相对隶属函数表示的模糊可变集合V。A＋、A－、A0分别称为模糊可变集合的吸引（为主）域、排斥（为主）域和渐变式质变界，V称为对立模糊集。

6．2．2　相对差异函数模型

1）相对差异函数定义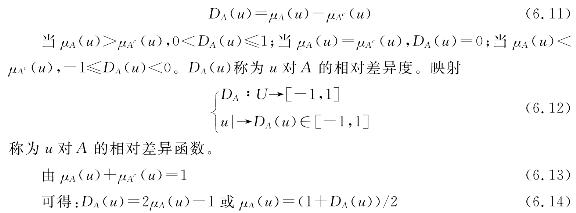

2）相对差异函数模型

设X0＝［a，b］为实轴上可变模糊集合V的吸引域，即0＜DA（u）≤1区间，X＝［c，d］包含X0（X0＞X）的某一上、下界范围域区间，见图6．12所示。

图6．12　点x、M与区间［a，b］、［c，d］的位置关系

根据可变模糊集合V定义可知［c，a］与［b，d］均为V的排斥域，即－1≤DA（u）＜0。设M为吸引域区间［a，b］中DA（u）＝1的点值，可根据实际情况按物理分析确定。x为X区间内的任意点的量值，则x落入M点左侧时，其相对差异函数模型为：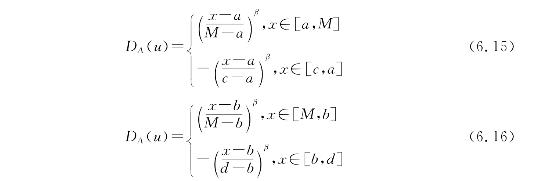

当β＝1时相对差异函数模型为线性函数，式（6．15）与（6．16）满足：

（1）当x＝a、x＝b时，DA（u）＝0；

（2）当x＝M时，DA（u）＝1；

（3）当x＝a、x＝b时，DA（u）＝－1。符合相对差异函数定义。DA（u）确定以后，根据式（6．14）可求解相对隶属度μA（u）。为了得到各指标的综合相对隶属度，应用式（6．17）模糊可变评价模型．

可变模型集包括陈守煜教授在工程模糊集理论中提出的模糊优选模型、模糊模式识别模型、模糊聚类循环迭代模型以及模糊决策、识别与聚类的统一模型等。可变模型参数集包括模型的指标权重、指标标准值等重要模型参数。引用陈守煜教授提出的可变模糊识别，

模型为：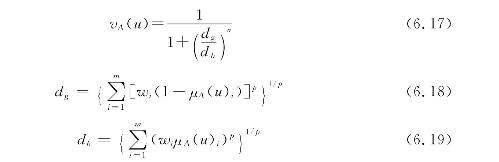

式中：μA（u）——事物u所具有的表征吸引性质A程度的相对隶属度；

wi——指标i的权重；

α——模型优化准则参数；

p——距离参数。

通常情况下模型中的α、p有4种搭配：

当α＝1，p＝2时，式（6．17）变为：

式（6．18）和式（6．19）中，取p＝2，即取欧式距离，此时式（6．21）相当于理想点模型，属于可变模糊集模型的一个特例。

当α＝1，p＝1时，式（6．17）变为：

式（6．22）相当于模糊综合评判模型，是一个线性模型，属于可变模糊集模型的又一个特例。

当α＝2，p＝1时，式（6．21）变为：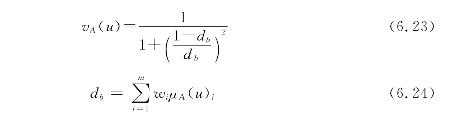

式（6．24）为Sigmoid型函数，可用以描述神经网络系统中神经元的激励函数。当α＝2，p＝2时，式（6．17）变为：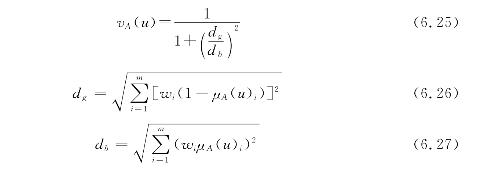

此时可变模糊集模型相当于模糊优选模型。由此可见，可变模糊集模型是一个变化模型，在可变模糊集理论中是一个十分重要的模型，可广泛应用于水文、水资源、水环境、水利水电等水科学工程领域的评价、识别、预测等问题。

6．2．3　评价指标与分级标准

干旱指标的确定是个非常复杂的问题，目前没有一个统一的标准。衡量一个地区是否属于干旱气候，一般用干燥指数，即蒸发势与降水量的比值。当干燥指数大于1，表示干旱、雨水不足；当干燥指数大于4，表示极端干旱。但是这样的指标在塔河来说过于笼统，在实践中，不同时间、不同地域有不同的干旱指标。从时间上划分有月、季、年等阶段性的干旱指标，从地域上划分有局地、区域、全区的干旱指标。用国家气候中心关于降水量的等级显然不能完全反映塔河流域的实际干旱情况，用河流径流量作为塔河的干旱指标比较切合实际，但是在分析以县级为单位的干旱风险评估，很多地方没有代表性的水文站。塔河流域的春旱是最严重的，发生的频率高，其次夏旱和秋旱也比较严重。根据《干旱评估标准》规范和塔河的干旱特点，本次干旱指标采用降水量距平法，农业旱灾等级采用综合减产成数法。

（1）降水量距平法的计算公式

式中：Dp——计算期内降水量距平百分比（%）；

P——计算期内降水量（mm）；

P——计算期内多年平均降水量（mm）。计算期内的多年平均降水量P 宜采用近30年的平均值。

计算期是根据不同季节选择适当的计算期长度。夏季宜采用1个月，春、秋季宜采用连续2个月，冬季宜采用连续3个月，从农牧业生产考虑，春旱、夏旱和秋旱是威胁最大的。因此本次采用塔河流域21个气象站点的1960—2008年降水量进行降水量距平分析。气象站点代表的县市见表6．2。春季降水距平D春表示春旱，计算时段采用4～5月；夏季降水距平D夏表示夏旱，计算时段采用6月；秋季降水距平D秋表示秋旱，计算时段采用9～10月；旱情等级划分按表6．3。

表6．3　降水距平百分比旱情等级划分

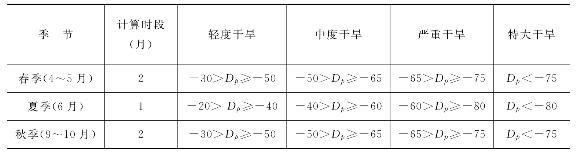
（2）综合减产成数法评估计算公式

C＝［I3×90%＋（I2－I3）×55%＋（I1－I2）×20%］×－1　（6．29）

式中：C——综合减产成数（%）；

I1——受灾（减产1成以上）面积占播种面积的比例（用小数表示）；I2——成灾（减产3成以上）面积占播种面积的比例（用小数表示）；I3——绝收（减产8成以上）面积占播种面积的比例（用小数表示）。

因为降水距平是负值，为了便于计算研究，将综合减产成数的和乘以－1，转化成与降水距平变化相一致的形式。旱灾等级划分见表6．4。综合减产成数法是一个综合干旱指标，该指标充分考虑了农业抗旱能力在干旱风险区划中的影响。农业抗旱能力受到自然、地域条件和人类活动等多方面因素的共同影响，对于塔河流域各县（市）抗旱能力也要从多方面综合判定。受灾面积、成灾面积、绝收面积占播种面积的比例能很好地代表抗旱因子对干旱风险评估的影响。

表6．4　农业旱灾等级划分表

6．2．4　干旱程度的确定

由于塔河流域主要受干旱的影响，利用流域内各县（市）的粮食减产率与有关统计资料相结合即可判定其实际干旱程度。

各种自然因素和非自然因素的综合影响形成了农作物的最终产量，相互间的关系极其复杂，很难用定量的量化关系来表述。国内外学者大都把这些因素按影响的性质、时间及尺度划分为农业技术措施、气象条件和随机“噪声”三大类。相应的，农作物产量也可以分解为趋势产量、气象产量和随机产量三部分。表达为：

式中：y——小麦的实际产量（kg/hm2）；

yt——小麦的趋势产量（kg/hm2）；

yw——小麦产量的气象产量（kg/hm2）；

Δy——小麦产量的随机分量（kg/hm2）。由于影响各地小麦增、减产的偶然因素并不时常发生，而且局地性的偶然因素的影响也不太大，因为在实际产量分解中，一般都假定Δy可忽略不计。式（6．30）可以简化为：

利用塔河流域各县（市）1990—2007年粮食产量资料进行分析，对趋势产量进行模拟，根据表6．2所列趋势产量方程，计算1990—2007年各县（市）的趋势产量。塔河流域88%县（市）的粮食产量曲线通过95%显著性检验。冬小麦减产率采用逐年的实际产量偏离趋势产量的相对气象产量的负值，计算公式为：

式中：yd——小麦减产率（%）；

y——实际产量（kg/hm2）

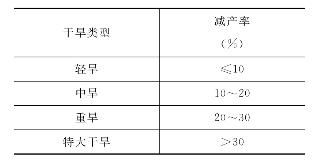
yt——趋势产量（kg/hm2）。根据表6．5粮食产量减产率定义1990—2007年每年的干旱程度，无旱、轻旱、中旱、重旱、特大干旱。根据粮食减产率和有关统计资料对塔河流域各县（市）干旱程度进行调整，作为塔河流域粮食生长时期内实际干旱情况，以便与其他指标对比。表6．6为粮食产量减产率的干旱等级。

表6．5　各个县市粮食趋势产量

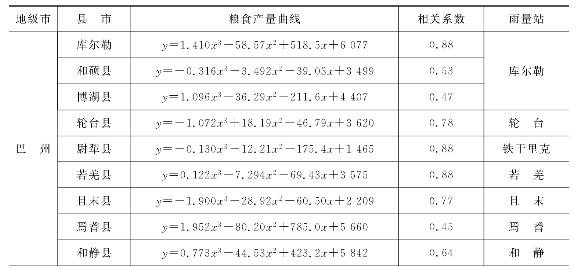
续表6．5

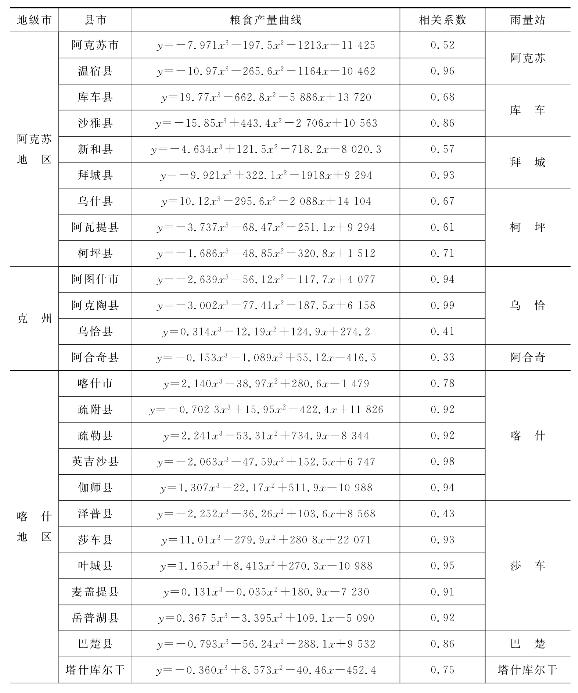
续表6．5

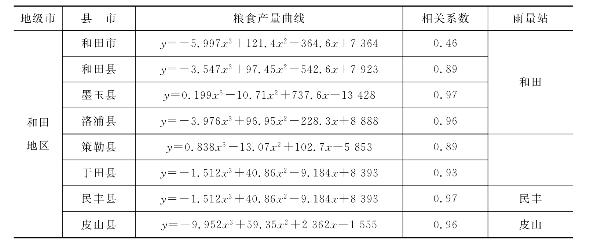
表6．6　粮食产量减产率的干旱等级

6．2．5　评价指标权重系数确定方法

权重确定的方法很多，在其他研究方法的思路上，结合塔河流域的干旱特点，采用级差加权指数法来确定干旱指数的权重，具体步骤是：假设已有某时段的干旱资料，将各个子模式干旱等级统一为无旱、轻旱、中旱、重旱、严重干旱五个等级，并定量化为0，1，2，3，4。然后根据某时段逐年出现的干旱实况划定各年的相应的干旱级别，将各个子模式计算的各年干旱级别与实况对照，并进行权重确定。权重计算公式为：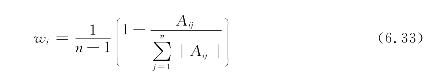

式中：wi——权重；

Aij——第i种干旱指标的模式在第j年计算的值与实测的值之差。

假设某时段的干旱资料是18年，将各个干旱指数的干旱级别分别统计为无旱、轻、中、严重、特大干旱5个等级，并量化为1，2，3，4，5。根据50年逐年出现的干旱实况划定各年的相应干旱级别（无旱、轻、中、严重、特大干旱），将各个干旱指数计算的各年干旱级别与实况对照，并进行权重的确定。计算过程见表6．7，计算得出的各县不同干旱指标的权重系数，见表6．8。干旱指标的权重系数见图6．13。从图中可以看出，不同县市的不同指标的权重是系数不同的，全流域综合减产成数的权重最大，其次是春季降水距平和夏季降水距平，秋季降水距平权重是最低的。春季降水距平权重的较高区域主要分布在巴州和阿克苏地区，喀喇昆仑山北麓县市的比重较低；夏季降水距平的较低区域主要是喀什地区，和田地区的夏季降水距平较高；除巴州和阿克苏地区外，其他地区秋季降水距平权重较高；综合减产成数较低的县市主要有皮山县、柯坪县、阿合奇县、若羌县，这些县（市）的农业播种面积较小，比如阿合奇县的播种面积仅多于3　000hm2，因此其综合减产成数的权重系数较低，阿克苏地区和喀什地区农业播种面积大，其对应的综合减产成数的权重系数低，因此级差加权指数法适合塔河流域干旱指标的权重系数计算。从图表中可以看出，各县市春、夏、秋季的降水距平的权重分布与各县市的春、夏、秋旱发生的频率一致。

表6．7　各干旱子模式的干旱等级计算成果

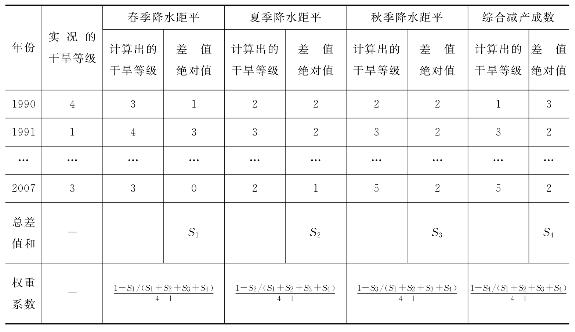
表6．8　各县（市）不同指标的权重系数

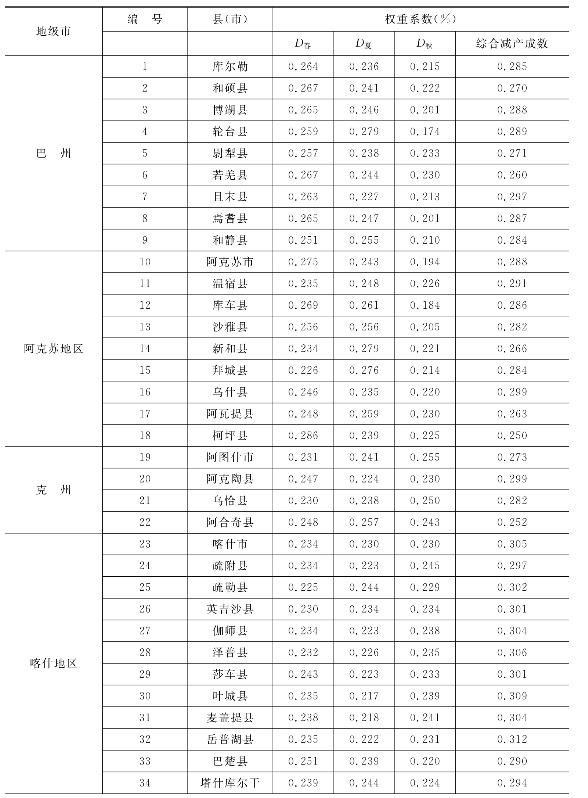
续表6．8

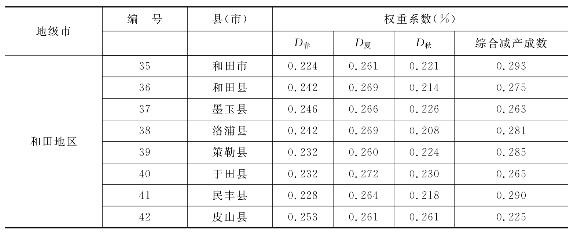
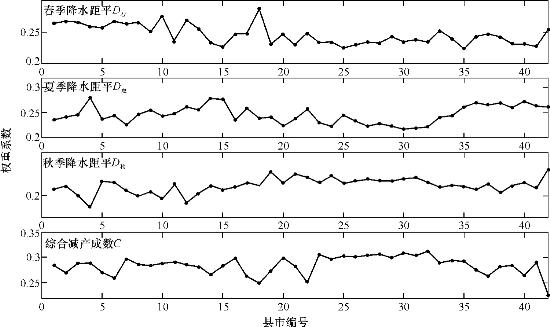
图6．13　塔河流域各县（市）干旱指标的权重系数

根据统计的塔河流域阿克苏地区、和田地区、喀什地区、巴州和克州5个地级市的42个县级市1990—2007年干旱发生的季节，塔河流域的春旱在4～5月，夏旱在6月，秋旱在9～10月发生干旱的频率高，本次采用的指标是：①春季降水距平D春的计算时段是4～5月；②夏季降水距平D夏的计算时段是6月；③秋季降水距平D秋的计算时段是9～10月；④综合减产成数C。因为降水距平是负值，为了便于计算研究，将综合减产成数的和乘以－1，转化成与降水距平变化相一致。

参照指标标准值和塔河流域的实际干旱指标情况确定干旱可变集合的吸引（为主）域矩阵与范围域矩阵以及点值Mih的矩阵分别为：

根据矩阵Iab、Icd与M判断样本特征值x在Mih点的左侧还是右侧，据此选用式（6．15）或式（6．16）计算差异度，再由式（6．17）计算指标对不同等级干旱的相对隶属度vA（u）。经过分析计算，α和p的取值对于各县（市）的不同年份的干旱程度基本没有影响，为了便于分析，本次采用α＝1和p＝1的可变模糊集模型来研究塔河流域干旱风险评估。塔河流域1990—2007年各县（市）的等级时空分布见图6．14～图6．16。

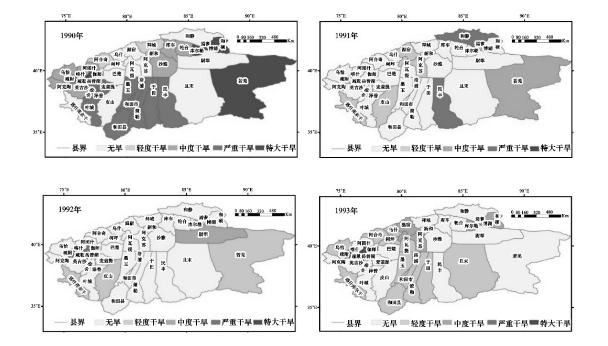
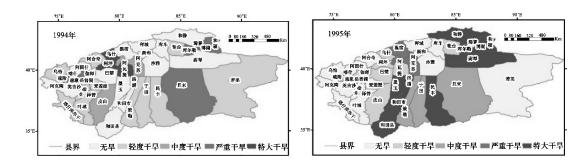
图6．14　塔河流域1990—1993年各县（市）干旱时空分布

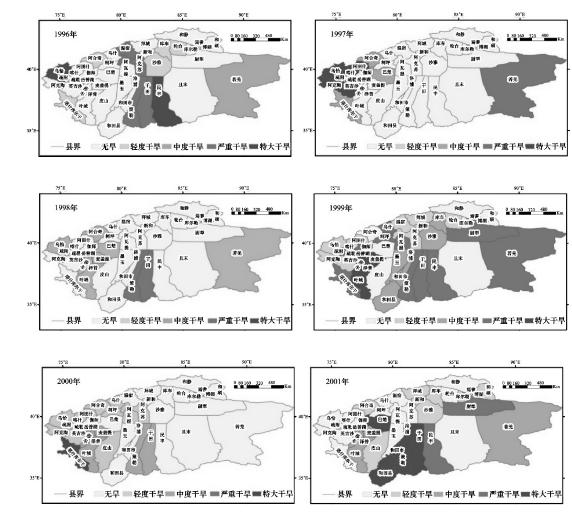
图6．15　塔河流域1996—2001年各县（市）干旱时空分布

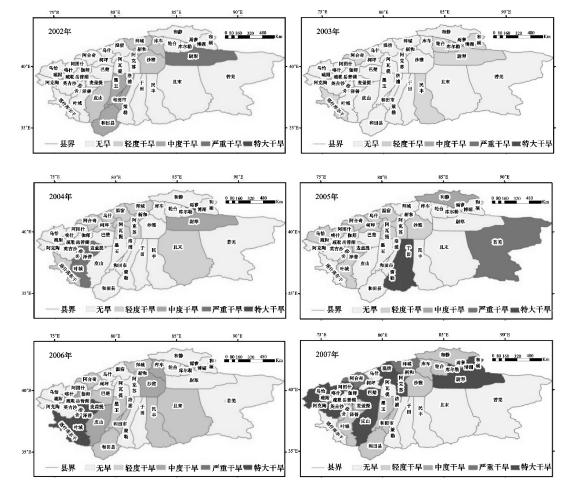
图6．16　塔河2002—2007年各县（市）干旱时空分布

图6．17是干旱等级趋势变化，塔河流域北部以及西南部地区干旱等级有呈增加的趋势，若羌等干旱地区干旱等级呈减小趋势。图6．18是基于可变模糊评价法的塔河流域农业干旱风险评估与气象干旱评估，由图知，轻度干旱发生频率最高的地区主要分布在塔河流域西北部地区，开孔河流域和喀什的部分地区的轻旱发生频率最低。塔河中游和若羌中旱发生频率最高，阿克苏地区的中旱发生频率最低，和田地区和喀什部分地区的中旱发生频率较高。重旱发生频率高的地区逐渐由塔河中游向下游地区转移，同时和田地区的策勒、于田、民丰和喀什地区的疏附、疏勒、伽师、英吉沙；重旱发生频率低的区域集中在巴州的库车、轮台、沙雅和塔河流域的西南部地区。虽然开孔河流域的轻、中、重旱发生频率较低，但是博斯腾湖附近特大干旱发生的概率较高，和田地区、喀什地区和克州特大干旱发生的概率较高。阿克苏地区特大干旱发生的频率是最低的。

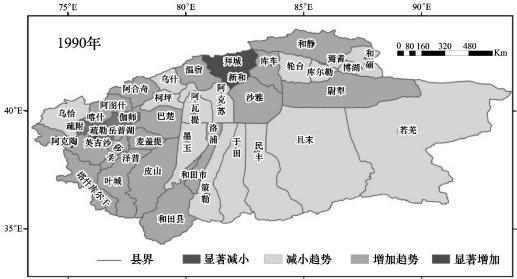
图6．17　塔河流域各县（市）干旱等级趋势变化

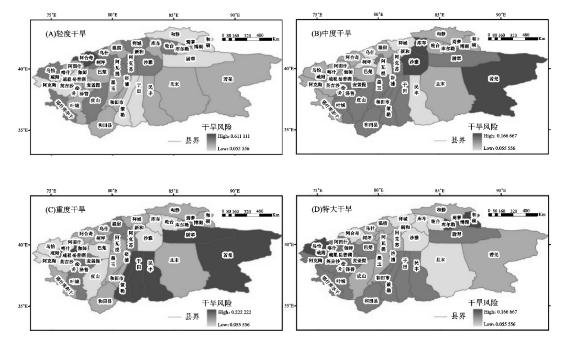
图6．18　塔河流域各县（市）不同干旱等级风险分布

6．3　本章小结

从气候干旱和农业干旱的角度出发，利用不同天数下的标准降雨指数SPI作为风险区划指标，根据选取的干旱指标进行干旱等级划分；采用基于可变模糊评价法对农业干旱风险进行评估；结合塔河流域的干旱特点，采用级差加权指数法确定干旱指数权重；分别对塔河流域各县（市）农业干旱风险和气象干旱做出了评估。