肿缩香肠构造的实验研究

第一节　肿缩香肠构造的实验研究

肿缩香肠构造虽然是最常见的香肠构造之一，但其形成过程及其条件仍未探讨清楚。本节介绍肿缩石香肠构造物理模拟，并引用Schmalholz和Maeder（2012）对肿缩香肠构造的二维有限元数值模拟结果，综合探讨肿缩香肠构造发育过程的规律。

一、物理模拟研究

实验材料主要由华中构造力学研究中心自行配制，其中，用作能干层的材料主要为橡胶腻子4^＃、5＃材料，部分实验是以红土或高岭土为能干层；用作基质的材料主要是以甲基乙烯基硅橡胶（下文表格中简称“甲基”）为主要原料配制的A10、A8材料，部分实验材料为凡士林；实验材料的部分流变参数由本课题组自行研制的夹心式流变仪测得（表5-1）。

表5-1　模型材料配方和流变参数表（23℃）

注：表中甲基的全称为甲基乙烯基硅橡胶。

实验所用装置如图3-8所示。实验过程简述如下：

（1）分别以均匀的基质、能干层材料做成基质、能干层的物理模型；测取能干层和基质层的初始厚度，一般能干层厚度为0.2～0.8cm，基质层的厚度为2～5cm。

（2）将能干层模型夹在基质层之间，放入装置内，Y方向上以玻璃板约束。

（3）在Z方向上均匀加载（图5-1），观察模型的变形。

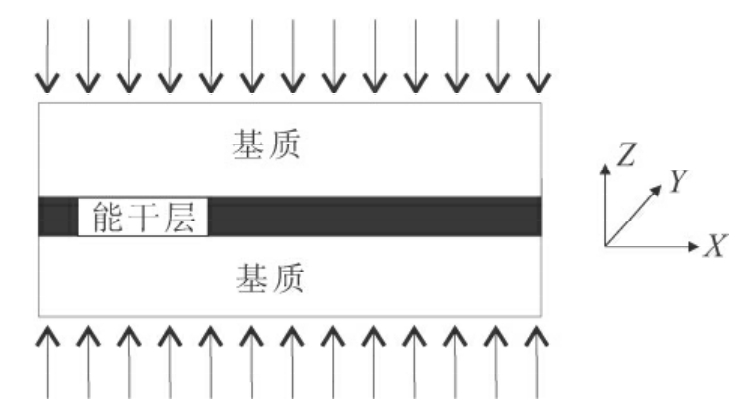
图5-1　香肠构造模拟实验示意图

由于橡胶腻子材料的韧性较大，实验中在部分橡胶腻子材料能干层上预加了初始扰动，即公式（4-5）中的Δh，其幅度一般为能干层厚度的5%±，间距较小，一般为2～3mm。这些初始扰动在变形过程中都会增大为颈缩部位，但其发育的程度却并不相同，颈缩的发生具有一定的规律，其波长与厚度的比值基本不变，与主波长理论相吻合。仔细观察肿缩香肠构造的变形特征，发现其颈缩部位的变形程度不一：强烈颈缩的呈近似相等的大间距排布，而其之间则有近于相等的较小间距排布的较弱颈缩变形（图5-3、图5-4）。认为这是能干层两期或者两期以上颈缩断裂的结果，虽然由于模拟实验中应变速率相对较大，香肠层肿缩断裂的先后次序表现得并不明显。

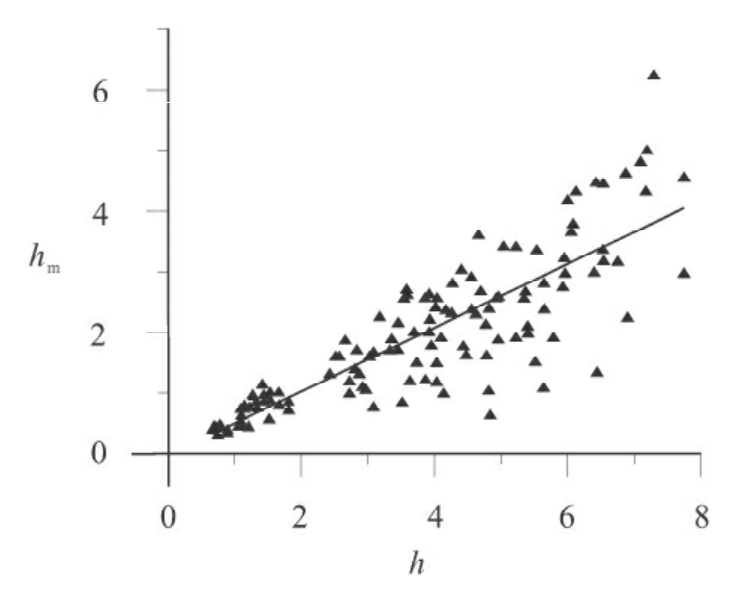
图5-2　物理模拟实验后香肠最大厚度（h_m）-颈缩部位厚度（h）投点图

本次研究共做物理模拟实验60多组。在h-hm图（图5-2）上可以看出，随着变形的发展，香肠构造膨胀部位的厚度和颈缩部位的厚度是基本成正比关系的。

图5-3　实验2、6、9的部分实验阶段照片基质均为A10，实验2、6的能干层为橡胶腻子5^＃，实验9的能干层为橡胶腻子4^＃；a为模型加载变形前；b为模型加载变形后

实验加载变形结束后（图5-3、图5-4），可以测得香肠构造的波长L、变形后的最大厚度hm以及颈缩部位的厚度h等相关参数，结合能干层初始厚度数据，可以运用公式（4-5）得到能干层的应力指数n_L；由于基质层应力指数n_M可取值1，再通过公式（4-3）可算得到基质和能干层的黏度比m（表5-2）。

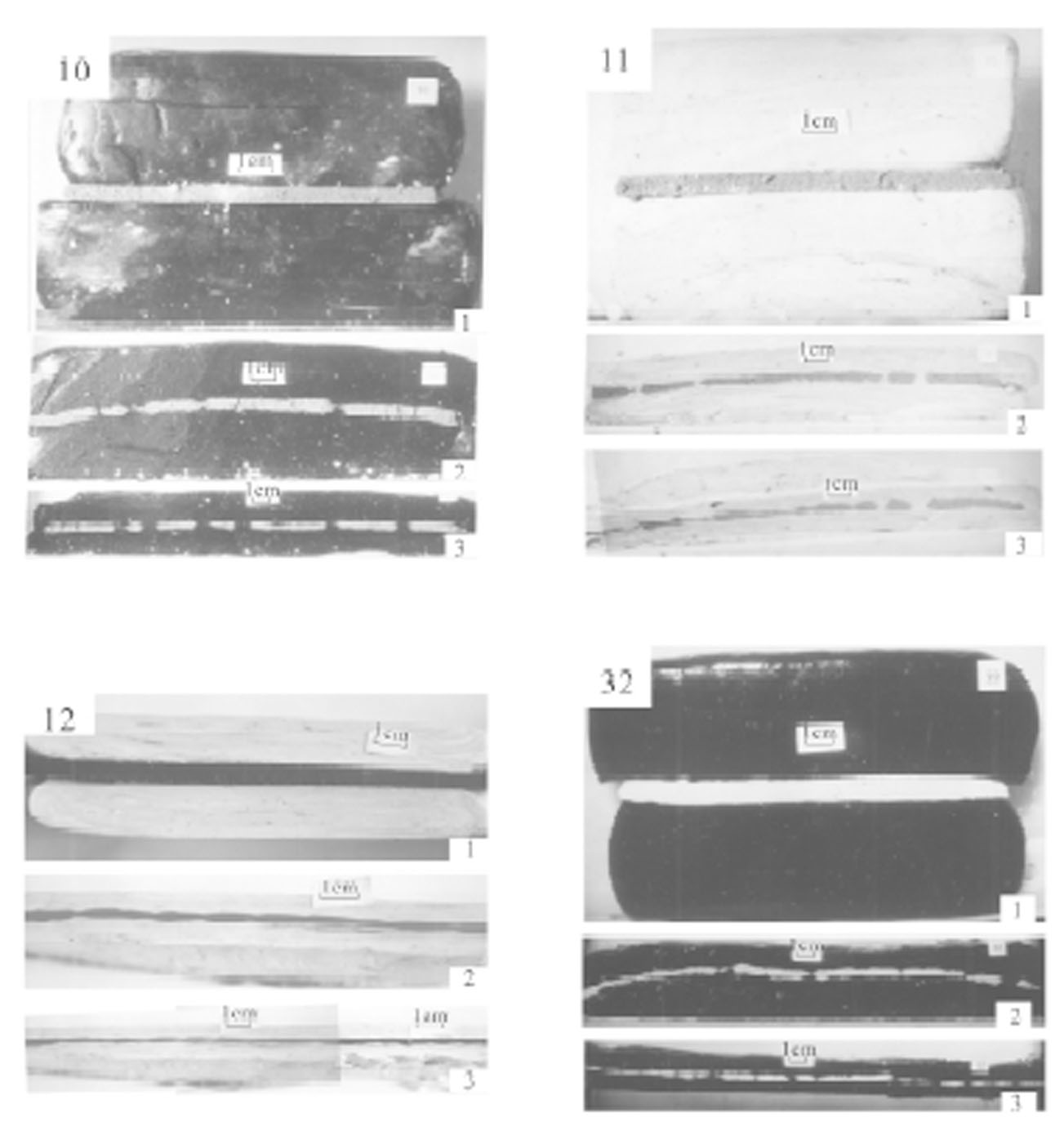
图5-4　实验10、11、12、32的部分实验阶段照片

实验11、12的基质为A10，能干层为红土；实验10、32的基质为A8，能干层为高岭土

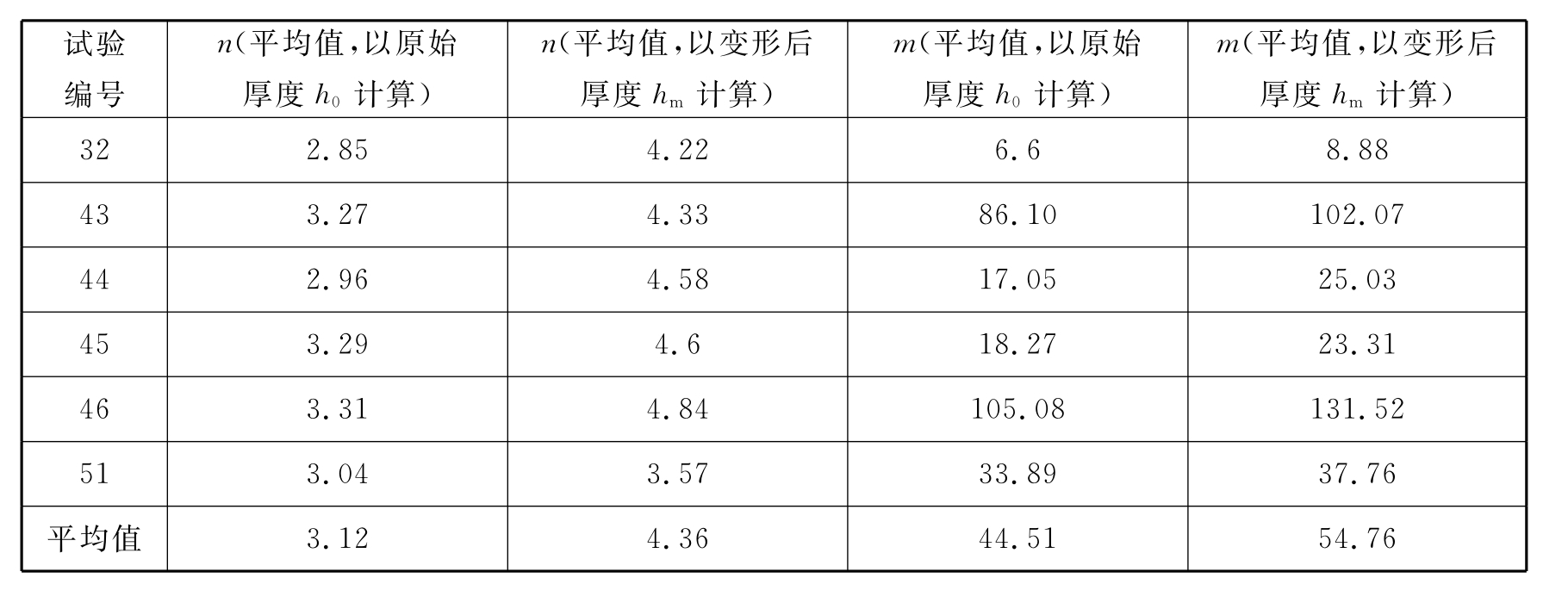
表5-2　部分物理模拟实验数据表

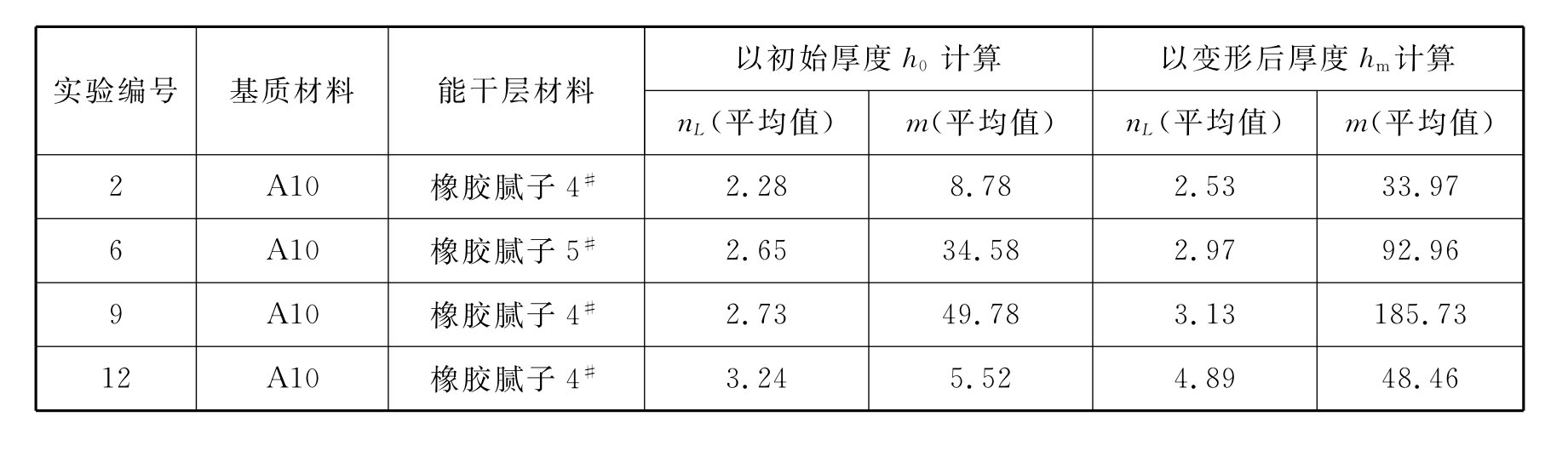
表5-2和表5-3表明：在不同基质层中，高岭土的应力指数变化不大，使用初始厚度得到的值为2.85～3.31，以变形后的最大厚度代替原始厚度得到的值为3.57～4.48；实测数据为2.69（表5-1），与使用初始厚度测算得到的吻合较好。在相同基质中，橡胶腻子4^＃的应力指数使用原始厚度与变形后厚度算得分别为2.28～3.24、2.53～4.89；实测应力指数2.08（表5-1），与通过初始厚度测算的值也更为吻合。可见使用原始厚度得到的应力指数值更接近实测值。Schmalholz和Maeder（2012）基于Hudleston和Treagus（2010）对单层褶皱的分析，认为肿缩香肠构造形成过程中的能干层与基质层黏度比多在10～100之间，这与本实验测算所得值的分布区间总体上相符（表5-2、表5-3）。上述分析也说明在从天然石香肠构造反演岩石流变学参数时，能干层初始厚度的恢复是很有必要的，这与前述对天然肿缩石香肠构造的理论研究结果相一致（详见第三章第一节）。

表5-3　高岭土在不同基质中计算得到的流变参数表

二、数值模拟研究

Schmalholz和Maeder（2012）利用二维非线性有限元数值模拟方法，分析了肿缩石香肠的形成。在其模型中，能干层为黏塑性体，屈服条件为冯·米塞斯准则，能干层和基质均表现幂律流体性质。研究表明，肿缩石香肠在黏度比介于10～20，应力指数介于1～5时，可以形成。实验中，能干层中的应力比等效屈服应力稍微偏小，由几何形态或者黏度差异导致的初始小扰动使得局部应力增加，从而局部塑性屈服。他们除详尽模拟单层能干层的肿缩香肠构造外，还模拟了多层能干层，以探讨多层肿缩香肠构造能否形成，以及是怎么形成的。

Schmalholz和Maeder（2012）的单层肿缩香肠构造模拟（图5-5）表明，能干层的缩颈作用从扰动位置开始发育，直至能干层变形前后长度比S值达到2左右时，能干层开始断开形成肿缩香肠构造，当S值达2.1时，颈缩部位经特征应力校正的偏差应力张量τⅡ/τ₀值逐渐增大，但其两侧肿大区的τⅡ/τ₀值却随之减小。该实验还表明，扰动的类型与形态对肿缩香肠构造的发育影响较小，但是起始扰动的大小则较为重要：扰动越大，发育肿缩香肠构造所需的S值就越小；反之，则越大。

将8组单层数值模拟实验数据投点到β-S图中（图5-6），可见，对于模型1，能干层与基质黏度比m值的减小（即较弱的颈缩不稳定性）会导致伴随伸展而发生减薄的速率变慢。对于所有基质幂律应力指数nM＝3的模型，减薄系数β值在S值很小时基本相一致。若基质层与能干层的幂律应力指数均表现为n_L＝n_M＝1的线性黏度，则只有当S＞3时，才能形成肿缩香肠构造；若没有塑性屈服的作用，则正如Smith（1977）所分析的，对于所赋予的m、n_L、nM值，颈缩不稳定性较弱，颈部的减薄速率只是略大于整个能干层的减薄，不能产生典型的肿缩石香肠构造。另外，对于相同的设定参数，模型2几何扰动导致的减薄速率快于模型1。在初始均匀减薄阶段（S≤1.2），各模型的减薄曲线都基本与纯剪切减薄模型的相一致。而初始均匀纯剪切减薄作用导致的伸展量受初始扰动大小的控制，即初始扰动越小，相应均匀纯剪切减薄作用导致的伸展范围越大；初始扰动越大，相应均匀纯剪切减薄作用导致的伸展范围越小，在图5-6中表现为减薄曲线相互分离的越快。

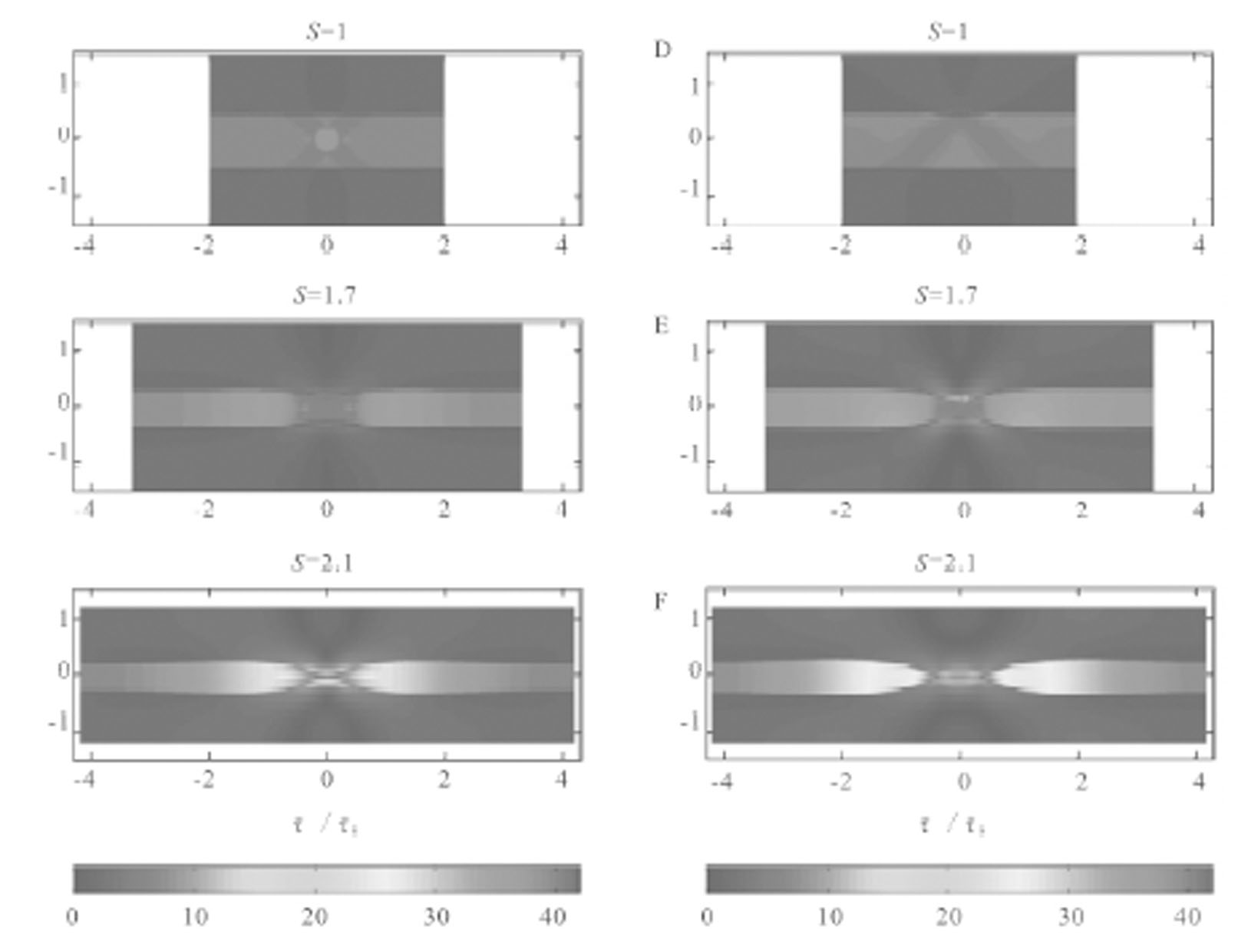
图5-5　两种不同扰动成因的单层肿缩香肠构造数值模拟（Schmalholz和Maeder，2012）

图A～C为能干层黏度差异扰动模型1，图A中能干层中段圆形区域黏度比其他区段小10%；图D～F为能干层形态不均扰动模型2，图D能干层中段上边界呈波幅为原始层厚1/50的正弦状；S为能干层变形前后的长度比，τ₀为特征应力（characteristic　stress），τ_Ⅱ为偏差应力张量（deviatoric　stress　tensor）；两模型的无量纲屈服应力为40.25，能干层与基质黏度比m＝20，能干层幂律应力指数n_L＝5，基质幂律应力指数n_M＝1

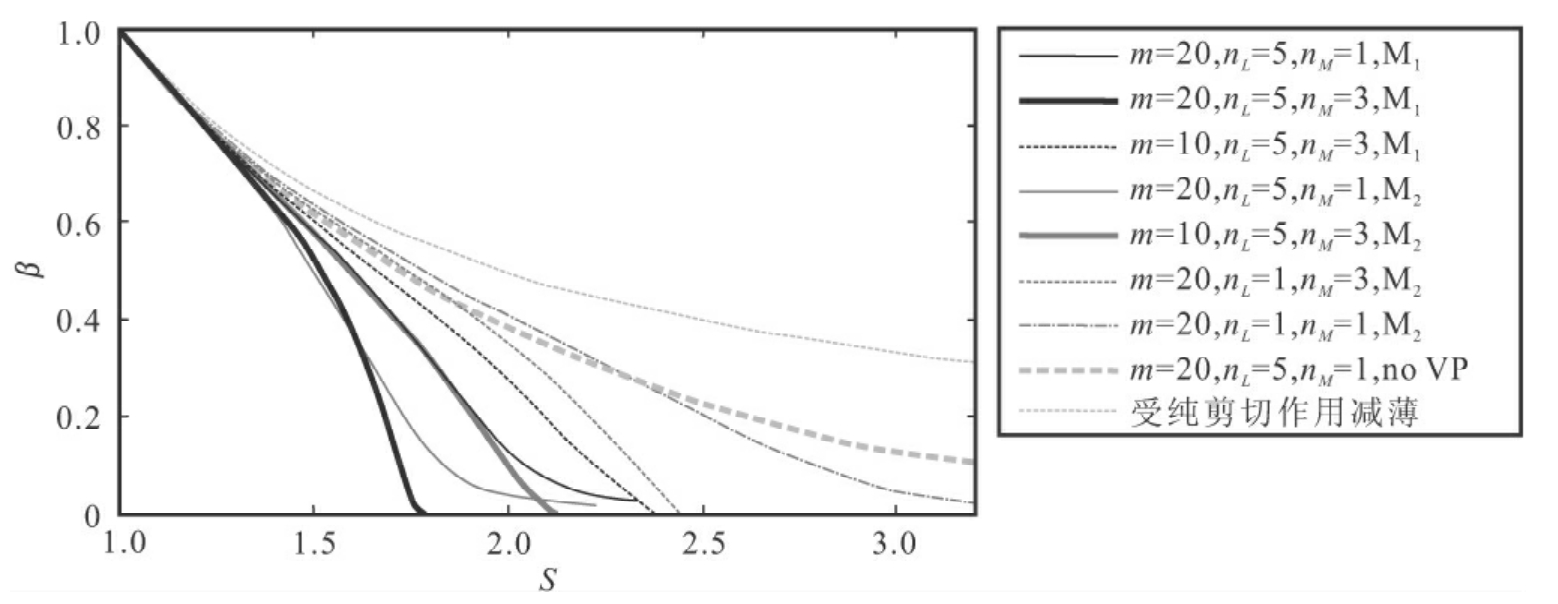
图5-6　八组单层数值模拟中减薄系数β（即颈缩处厚度与初始厚度之比）-长度比S关系图（据Schmalholz和Maeder，2012）m为能干层与基质层的厚度比；n_L、n_M分别为能干层与基质层的幂律应力指数；“no　VP”表示没有冯·米赛斯塑性作用；M₁、M₂分别对应设定的初始扰动模型1、2（详见图5-5）

图5-7～图5-9显示的是三组代表性的具有随机边界几何扰动的单层与多层肿缩香肠构造模拟。其中，在每个边界数值节点上的初始几何扰动随机生成，经扩散算法数值平滑后，形成波幅不超过初始厚度的1/33的初始扰动（Schmalholz和Maeder，2012）。

图5-7　能干层上下边界具有随机几何扰动的单层肿缩香肠构造数值模拟（Schmalholz和Maeder，2012）

m＝15，n_L＝3且n_M＝3；无量纲屈服应力为30.25；上下基质层厚度为3（通过能干层厚度校正），为便于观察，图中只给出其部分厚度（蓝色部分）；该实验最大总伸长度为270%

他们的单层模拟实验（图5-7）表明，单层中的肿缩香肠构造并非一定是同期形成的，当能干层在初始扰动导致差异减薄所形成的肿缩香肠体长宽比值还比较大（本实验中大于6±），长宽比值较大的肿缩香肠体将继续从其中段部分强烈减薄，进一步形成长宽比值较小的肿缩香肠构造，如此反复，直至所有肿缩香肠体长宽比值足够小（Shmalholz和Maeder，2012）。

对于三层能干层数值模拟实验（图5-8），由于最薄能干层的扰动不稳定性相对最大，因此，其最快形成肿缩香肠构造；继续伸展一段时间后，三层能干层开始整体上作为一层变形发育两颈缩区段，并在颈缩区由于剪切作用而形成了正断层，单层能干层也随之发生局部弯曲（Schmalholz和Maeder，2012）。

图5-9进一步表明，在相似的变形条件下，多层能干层相邻的变形不同于单层的肿缩化变形，其在初期的各单层能干层的颈缩化作用的进一步发展下，逐渐形成相交于最底部能干层的平直共轭正断层；随着变形的进一步发展，正断层下盘断面渐向上凸起，使得多层能干层一起整体上逐渐表现为肿缩香肠化，与他们在野外观察到的现象一致（Schmalholz和Maeder，2012）。

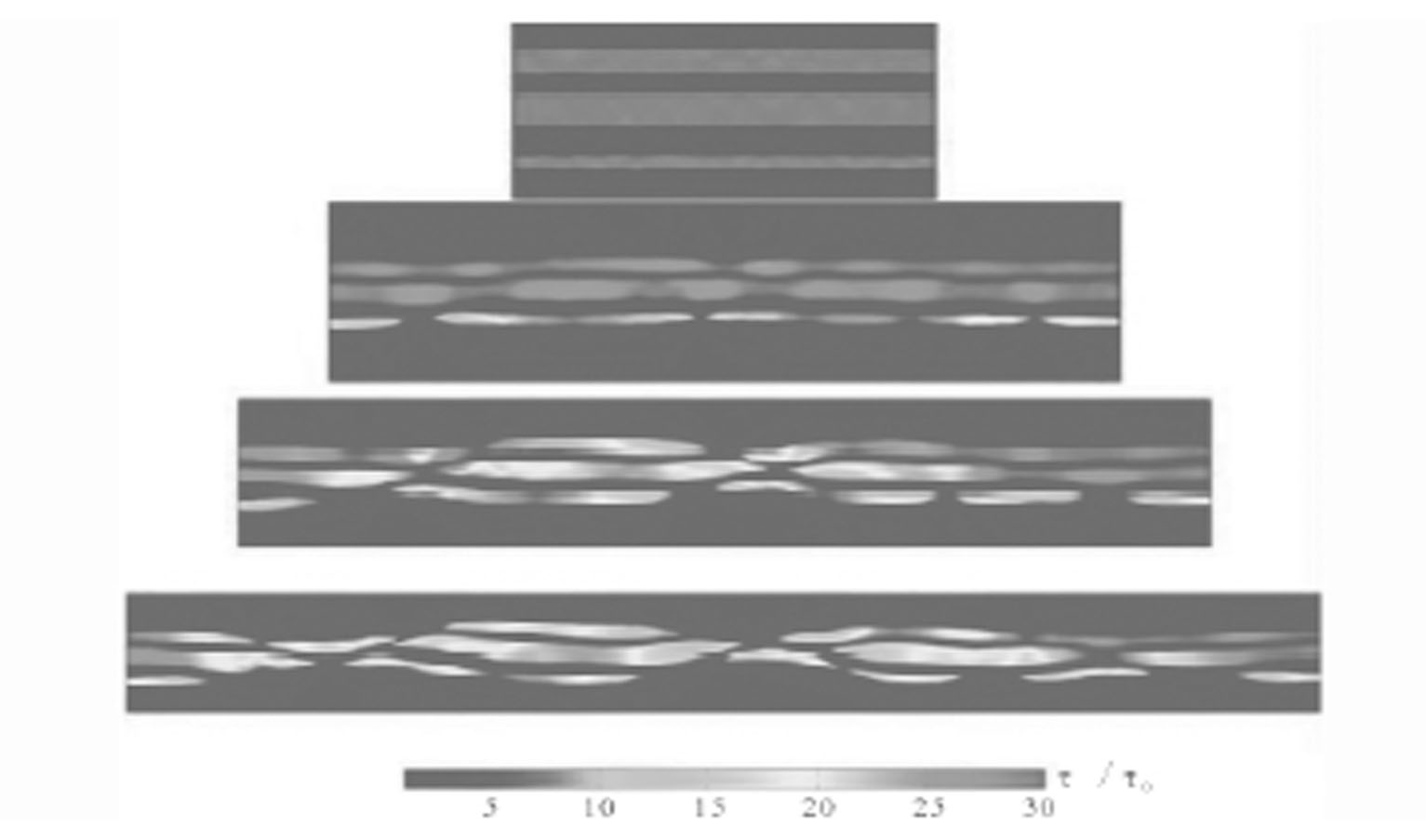
图5-8　能干层上下边界具有随机几何扰动的三层肿缩香肠构造数值模拟（Schmalholz和Maeder，2012）

对图中所有能干层与基质层：m＝15，n_L＝5且n_M＝3；无量纲屈服应力为30.25；基质层厚度自下至上依次为3、0.5、0.75、3（通过能干层厚度校正），为便于观察，图中只给出了部分厚度（蓝色部分）；能干层厚度自下至上依次为0.5、1、0.75

图5-9　能干层上下边界具有随机几何扰动的九层肿缩香肠构造数值模拟（Schmalholz和Maeder，2012）

对所有能干层与基质层：m＝20，n_L＝5且n_M＝3；无量纲屈服应力为40.25；图中百分数为总伸长度（1-S）；上下基质层厚度为6，其他的为0.5（通过能干层厚度校正），为便于观察，图中只给出了部分厚度（蓝色部分）；能干层厚度均为1

三、分析与结论

当能干层与基质层的黏度比较小（10～20）且幂律应力指数也较小（1～5）时，肿缩香肠构造可在表现出幂律定律流变和等效屈服应力的黏塑性能干层中发育（Schmalholz和Maeder，2012）。

肿缩香肠构造的形成是在纯剪切作用下，由于其颈缩区物质黏度、几何形态不均一等扰动导致形成的。其颈缩作用同时也会导致应变局部化，同时能干层颈缩区应力逐渐相对增大，而其两侧能干层肿大区应力随之逐渐减小。

肿缩香肠构造的数值模拟表明其可不同尺度（包括单层与多层能干层的规模）地发育。虽然都是处于总体的纯剪切作用下，不同于单层能干层肿缩香肠化变形，多层能干层的肿缩香肠化会伴随有剪切带的形成，剪切面由相邻能干层的颈缩区相连并斜交于层面产出（Schmalholz和Maeder，2012）。

物理模拟和数值模拟均表明，同一层中的肿缩香肠构造不一定是同期形成的，长宽比较大的肿缩香肠体可在平行层面的伸展作用下，从其中段进一步肿缩香肠化直至长宽比值足够小；也均进一步证明了Hudleston和Treagus（2010）关于肿缩香肠构造变形过程中能干层与基质层黏度比多在10～100区间内的认识。

这里还需要补充的是肿缩石香肠与透镜状石香肠，Goscombe等（2004）称之为锥角状石香肠（tapering　boudins）的异同点（表2-1）。透镜状石香肠虽然也普遍发育，但一般认为它是由于肿缩石香肠颈缩断开后继续顺层伸展形成的（Goscombe等，2004），也属于典型的韧性石香肠。部分学者所理解的肿缩石香肠概念中包含有透镜状石香肠（Schmalholz，2008；Schmal-holz和Maeder，2012）。但前面章节介绍的利用肿缩香肠构造恢复岩层初始厚度与计算岩层的流变参数的方法原理，并不能很好地适用于透镜状石香肠，因为一方面透镜状石香肠的发育意味着能干层伸长率较大，易导致测算到的岩层初始厚度值偏离真实值较大；另一方面透镜状石香肠的颈缩部位厚度减薄拉断至厚度为0，不能应用公式（4-5），故表2-1将透镜状石香肠作为独立端员划分出来。另外，鉴于其与肿缩石香肠的相似性，并且本节试验研究中，部分“肿缩石香肠”实际为透镜状石香肠或者向其过渡的类型（图5-3～图5-5、图5-7、图5-8），故本节实验研究得出的大多数认识仍适用于透镜状石香肠构造。